Tìm tất cả các số thực x,y để hai số phức là hai số phức liên hợp của nhau.
A. ![]() .
.
B. ![]() .
.
C.![]() .
.
D.![]()
Tìm tất cả các số thực x, y để hai số phức z 1 = 9 y 2 - 4 - 10 x i 5 , z 2 = 8 y 2 + 10 i 11 là hai số phức liên hợp của nhau.
A. x = 2 y = ± 2
B. x = ± 2 y = 2
C. x = - 2 y = ± 2
D. x = - 2 y = 2
Cho x,y là các số phức ta có các khẳng định sau:
1) x + y ¯ v à x ¯ + y là hai số phức liên hợp của nhau.
2) x y ¯ v à x ¯ y là hai số phức liên hợp của nhau.
3) x − y ¯ v à x ¯ − y là hai số phức liên hợp của nhau.
Hỏi có bao nhiêu khẳng định đúng
A. không
B. một
C. hai
D. ba
Tìm số thực x; y để hai số phức z1 = 9y2 – 4 – 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau?
A. x = -2; y = 2.
B. x = 2; y = ±2.
C. x = 2; y = 2.
D. x = -2; y = ±2.
Chọn D.
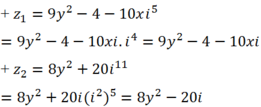
+ z1 và z2 là liên hợp của nhau khi và chỉ khi:
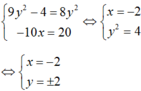
Tìm số thực x,y để hai số phức z1 = 9y2 - 4 - 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau? z 1 = 9 y 2 - 4 - 10 x i 5 v à z 2 = 8 y 2 + 20 i 11 l à
A. x = -2; y = 2.
B. x = 2; y = ±2.
C. x = 2; y = 2.
D. x = -2; y = ±2.
Cho hai số phức z 1 = a + 8 b + 20 i 3 , z 2 = 9 b - 4 - 10 a i Tìm a, b để z 1 , z 2 là liên hợp của nhau.
A. a = 2; b = 2
B. a = -2; b = 6
C. a = 2; b = 6
D. a = -2; b = 2
Cho hai số phức z,z’. Cặp số nào sau đây không là hai số phức liên hợp của nhau?
A . z + z ' v à z + z '
B . z z v à z z '
C . z - z v à z - z '
D . z z ' v à z z '
Xét phương trình bậc hai az2+bz+c=0 trên tập C a ≠ 0 , a , b , c ∈ R . Tìm điều kiện cần và đủ để phương trình có hai nghiệm z1 và z2 là số phức liên hợp với nhau.
![]()
![]()
![]()
![]()
Phần thực của số phức z = 2 + 3 i 200 có dạng a 2 + b 3 + c 6 + d với a, b, c, d là các số nguyên. Trong các số a, b, c, d có tất cả bao nhiêu số bằng 0
A. 3
B. 1
C. 4
D. 2
Ta có ![]()
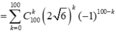
Phần thực của z tương ứng với k là bội của 2, vậy phần thực bằng
![]()
![]() là một số nguyên dương.
là một số nguyên dương.
Chọn đáp án A.
Phần thực của số phức z = 2 + 3 i 200 có dạng a 2 + b 3 + c 6 + d với a, b, c, d là các số nguyên. Trong các số a, b, c, d có tất cả bao nhiêu số bằng 0.
A. 3.
B. 1.
C. 4.
D. 2.