Số trung bình của dãy số liệu 1;1;2;3;3;4;5;6;7;8;9;9;9 gần đúng với giá trị nào nhất trong các giá trị sau?
A. 5,14
B. 5,15
C. 5
D. 6
Cho dãy số liệu (1) : a1; a2; a3...an-1; an trong đó a1; a2; ..an là các số cho trước có số trung bình cộng là x1
Và cho dãy số liệu (2): a1 - 1; a2; a3...an-1; an+ 1 có số trung bình cộng là x2
Chọn mệnh đề đúng?
A. x1 = x2
B. x1 > x2
C. x1 < x2
D. Không só sánh được
Chọn A.
Dãy số liệu thứ 2 có 2 số liệu khác với dãy số liệu 1 là số đứng ở vị trí đầu tiên và số đứng ở vị trí cuối cùng. Tuy nhiên tổng của số đứng đầu tiên + số đứng ở vị trí cuối cùng không thay đổi. Do đó; số trung bình không thay đổi.
Cho dãy số liệu thống kê: 21, 23, 24, 25, 22, 20, 27, 28. Số trung bình cộng của dãy số liệu thống kê đã cho là
A. 23,57
B. 23,75
C. 19
D. 22,57
Chọn B.
Số trung bình của dãy số liệu thống kê đã cho là:
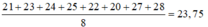
Cho dãy số liệu thống kê (đơn vị là kg): 1, 2, 3, 4, 5 (1)
Dãy (1) có trung bình cộng x = 3kg và độ lệch chuẩn s = 2 kg.
Cộng thêm 4 kg vào mỗi số liệu thống kê của dãy (1), ta được dãy số liệu thống kê (đã hiệu chỉnh) sau đây (đơn vị là kg): 5, 6, 7, 8, 9.(2)
Khi đó ta có: Độ lệch chuẩn của dãy (2) là:
A. 2 kg
B. 3 kg
C. 4 kg
D. 6 kg
Cách 1. Ta có: Khi cộng vào mỗi số liệu của một dãy số liệu thống kê cùng một hằng số thì phương sai và độ lệch chuẩn không thay đổi. Do đó độ lệch chuẩn của dãy (2) vẫn là 2 kg.
Cách 2. Tính trực tiếp độ lệch chuẩn của dãy (2).
Đáp án: A.
Cho dãy số liệu thống kê : 21, 23, 24, 25, 22, 20
Số trung bình cộng của các số liệu thống kê đã cho là bao nhiêu ?
Số trung bình cộng của các số liệu thống kê đã cho là 22,5
Tính số trung bình của dãy số liệu trong bảng 5 bằng hai cách: sử dụng bảng phân bố tần số và sử dụng bảng phân bố tần suất (theo các lớp chỉ ra trong bài tập 2 – bài 1).
Tính chiều cao trung bình của học sinh nam
Cách 1: Sử dụng bảng phân bố tần số ghép lớp
x− = (5 x 140 + 9 x 150 + 19 x 160 + 17 x 170 + 10 x 180) / 60
x− = 163
Cách 2: Sử dụng bảng phân bố tần suất ghép lớp
x− = (8,33 x 140 + 15 x 150 + 31,67 x 160 + 28,33 x 170 + 16,67 x 180) / 100
x− = 163
Tính chiều cao trung bình của học sinh nữ
Cách 1. Sử dụng bảng phân bố tần số ghép lớp
x− = (8 x 140 + 15 x 150 + 16 x 160 + 14 x 170 + 7 x 180) / 60
x− = 159,5
Cách 2: Sử dụng bảng phân bố tần suất ghép lớp
x− = (13,33 x 140 + 25 x 150 + 26,67 x 160 + 23,33 x 170 + 11,67 x 180) / 100
x− = 159,5
Bài. Tính trung bình cộng các phần tử trong dãy Cho dãy số nguyên gồm N phần tử a1, a2, …, aN
Yêu cầu: Tính trung cộng các phần tử trong dãy. Dữ liệu vào: File văn bản AVG.INP gồm + Dòng đầu ghi số N ; + Dòng thứ hai một dãy số nguyên a1, a2, …, aN (mỗi số cách nhau ít nhất một dấu cách). Dữ liệu ra: Ghi ra file văn bản AVG.OUT + Một số duy nhất là trung bình cộng các phần tử trong dãy(làm tròn một chữ số thập phân).
#include <bits/stdc++.h>
using namespace std;
long long a[10000],i,n,t;
int main()
{
freopen("avg.inp","r",stdin);
freopen("avg.out","w",stdout);
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
t=0;
for (i=1; i<=n; i++) t+=a[i];
cout<<fixed<<setprecision(1)<<(t*1.0)/(n*1.0);
return 0;
}
Cho dãy số 1; 4; 10; ...100; 103
a) Tìm số trung bình cộng của các số trong dãy
b) Tìm số trung bình cộng của các số chẵn trong dãy đó
Nếu số số hạng của một dãy số là một số lẻ thì trung bình cộng của tất cả trong dãy số là.....
Nếu số số hạng của một dãy số là một số chẵn thì trung bình cộng của tất cả trong dãy số là.....
trung bình cộng là một số thập phân
Tìm trung bình cộng của dãy số sau, biết dãy số có 20 số hạng 2; 6; 10; 14; 18; ...... Vậy trung bình cộng của dãy số trên là:
Dãy số đấy không thể có 20 số hạng đươc
Số số hạng của dãy là : (18-2):2+1=9[ ( số cuối - số đầu ) : khoảng cách giữa hai số liên tiếp +1]
Tổng của dãy là : (18+2).9:2 = 90 [ ( số cuối + số đầu ) .số số hạng : 2]
Trung bình cộng của dãy trên là : 90 :9 = 10 ( tổng : số hạng )
Đáp số : 10