Cho a, b là hai số thực dương và a ≠ 1 thỏa mãn log a b = 2 . Tính giá trị biểu thức P = log a 2 b b 2 a
A. P = 2 + 3 2 2
B. P = 2 2 2 + 1
C. P = 2 - 1 2 + 1
D. P = - 6 + 5 2 2
Những câu hỏi liên quan
SGK Cánh Diều
13 tháng 8 2023 lúc 21:10
Đề bài
Cho hai số thực dương a, b thỏa mãn \({a^3}{b^2} = 100\). Tính giá trị của biểu thức \(P = 3\log a + 2\log b\)
\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)
Đúng 0
Bình luận (0)
Cho a,b,c là các số thực dương thỏa mãn
a
log
5
2
4
,
b
log
4
6
1
,
log
,
c
log
7
3
49
Tính giá trị của biểu thức
T
a...
Đọc tiếp
Cho a,b,c là các số thực dương thỏa mãn a log 5 2 = 4 , b log 4 6 = 1 , log , c log 7 3 = 49 Tính giá trị của biểu thức T = a log 2 2 5 + b log 4 2 6 + 3 c log 7 2 3
A. T=126
B. T = 5 + 2 3
C. T=88
D. T = 3 - 2 3
Cho a, b là hai số thực dương và
a
≠
1
thỏa mãn
log
a
b
2
.
Tính giá trị biểu thức
P
log...
Đọc tiếp
Cho a, b là hai số thực dương và a ≠ 1 thỏa mãn log a b = 2 . Tính giá trị biểu thức P = log a 2 b b 2 a .
A. P = 2 + 3 2 2 .
B. P = 2 2 2 + 1 .
C. P = 2 - 1 2 + 1 .
D. P = − 6 + 5 2 2 .
Cho a, b là hai số thực dương và
a
≠
1
thỏa mãn
log
a
b
2
Tính giá trị biểu thức
P
log
a
2
b
b
2
a
A.
P
...
Đọc tiếp
Cho a, b là hai số thực dương và a ≠ 1 thỏa mãn log a b = 2 Tính giá trị biểu thức P = log a 2 b b 2 a
A. P = 2 + 3 2 2
B. P = 2 2 2 + 1
C. P = 2 - 1 2 + 1
D. P = - 6 + 5 2 2
Cho a, b là hai số thực dương khác 1 và thỏa mãn
log
2
a
b
-
8
log
b
a
b
3
-
8
3
. Tính giá trị biểu thức
P
log
a
a
a...
Đọc tiếp
Cho a, b là hai số thực dương khác 1 và thỏa mãn log 2 a b - 8 log b a b 3 = - 8 3 . Tính giá trị biểu thức P = log a a a b 3 + 2017 .
A. P = 2019
B. P = 2020
C. P = 2017
D. P = 2016
Đáp án A
Ta có log 2 a b - 8 log b - 8 3 ⇔ log a b 2 - 8 log b a - 8 3 = - 8 3 ⇔ log a b 3 = 8 ⇔ log a b = 2
Khi đó P = log a a a b 3 + 2017 = log a a 4 3 . b 1 3 + 2017 = 4 3 . log a a + 1 3 . log a b + 2017 = 4 3 + 2 3 + 2017 = 2019 .
Đúng 0
Bình luận (0)
Cho a, b là hai số thực dương khác 1 và thỏa mãn
log
a
2
b
-
8
log
b
(
a
b
3
)
-
8
3
. Tính giá trị biểu thức P
log
a
(...
Đọc tiếp
Cho a, b là hai số thực dương khác 1 và thỏa mãn log a 2 b - 8 log b ( a b 3 ) = - 8 3 . Tính giá trị biểu thức P = log a ( a a b 3 ) + 2017
A. P = 2019
B. P = 2020
C. P = 2017
D. P = 2016
Giả sử a, b là các số thực sao cho x3 + y3 a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) z và log(x2 + y2) z + 1. Giá trị của a+b bằng: A.
-
31
2
B.
-
25
2
C.
31
2
D.
29
2
Đọc tiếp
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Đáp án D.
Ta có
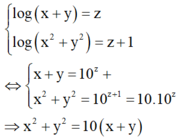
Khi đó
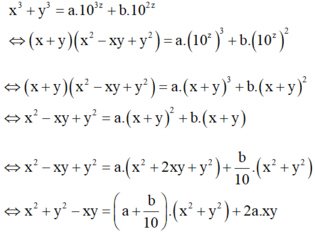
Đồng nhất hệ số, ta được
Đúng 0
Bình luận (0)
Cho hai số thực dương a, b thỏa mãn
9
a
3
+
a
b
+
1
3
b
+
2
. Giá trị lớn nhất của biểu thức S 6a - b là A.
17
12
B.
82
3
C. ...
Đọc tiếp
Cho hai số thực dương a, b thỏa mãn 9 a 3 + a b + 1 = 3 b + 2 . Giá trị lớn nhất của biểu thức S = 6a - b là
A. 17 12
B. 82 3
C. 11 3
D. 89 12
Đáp án C
Ta có: 9 a 3 + a b + 1 = 3 b + 2 ⇔ 9 a 3 + a = b + 1 3 b + 2
Đặt t = 3 b + 2 ⇒ b = t 2 - 2 3 ⇒ 9 a 3 + a = t 2 + 1 3 t ⇔ 27 a 3 + 3 a = t 3 + t ⇔ 3 a 3 + 3 a = t 3 + t
Xét hàm số f u = u 3 + u u ∈ ℝ ⇒ f ' u = 3 u 2 + 1 > 0 ∀ u ∈ ℝ ⇒ f u đồng biến trên ℝ
Khi đó: f 3 a = f t ⇔ t = 3 a ⇒ 3 b + 2 = 3 a ⇔ b = 9 a 2 - 2 3
Suy ra S = 6 a - 3 a 2 + 2 3 = - 3 a - 1 2 + 11 3 ≤ 11 3 .
Do đó giá trị lớn nhất của biểu thức S = 6a - b là 11 3 .
Đúng 0
Bình luận (0)
Cho hai số thực dương a; b thỏa mãn log2(a + 1) + log2(b + 1) ≥ 6 Giá trị nhỏ nhất của biểu thức S = a + b là
A.12
B.14
C. 8
D.16
Chọn B.
Ta có 6 ≤ log2(a + 1) + log2(b + 1) = log2[(a + 1)(b + 1) ]
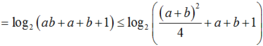
Suy ra: 
hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
Tương đương: (a + b) 2 + 4(a + b) - 252 ≥ 0
Suy ra: a + b ≥ 14
Đúng 0
Bình luận (0)