Một vật dao động điều hòa dọc theo trục Ox với phương trình dao động là x = 4 cos ( 2 πt - π / 3 ) cm (t tính bằng s). Lấy π 2 = 10 . Gia tốc của vật khi có li độ bằng 3 cm là
A. ‒12 cm/s2
B. 120 cm/s2
C. ‒1,2 cm/s2
D. ‒60 cm/s2
Một vật nhỏ dao động điều hòa dọc theo trục Ox có phương trình dao động là x = 12cos(2πt + π/3) cm. Biên độ dao động của vật là
A. 6 cm
B. 6 2 cm
C. 3 cm
D. 12 cm
Biên độ dao động của vật A = 12cm
Đáp án D
Một vật nhỏ dao động điều hòa dọc theo trục Ox có phương trình dao động là x = 12cos(2πt + π/3) cm. Biên độ dao động của vật là
A. 2π cm.
B. 6 cm.
C. π/3 cm.
D. 12 cm
Đáp án D
+ Biên độ dao động của vật A=12cm
Một vật nhỏ dao động điều hòa dọc theo trục Ox có phương trình dao động là x=12cos(2πt+π/3) cm. Biên độ dao động của vật có giá trị là
A. 6 cm.
B. 2π cm.
C. π/3 cm.
D. 12 cm.
Đáp án D
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hoà
PT dao động x = 12cos(2πt + π/3) cm => Biên độ dao động A = 12cm
Một vật nhỏ dao động điều hòa dọc theo trục Ox (vị trí cân bằng ở O) với biên độ 4 cm và tần số 10 Hz. Tại thời điểm t = 0, vật có li độ 4 cm. Phương trình dao động của vật là A.x = 4cos(20 π t + π ) cm. B.x = 4cos20 π t cm. C.x = 4cos(20 π t – 0,5 π ) cm. D.x = 4cos(20 π t + 0,5 π ) cm.
Một vật dao động điều hòa dọc theo trục Ox với phương trình vận tốc là overline v = 16π cos(4πt - π/6) cm/ s . Xác định thời điểm lần thứ 2023 vật chuyển động nhanh dần qua vị trí x =2 kể từ lúc bắt đầu dao động
Từ pt \(v=16\pi\cos\left(4\pi t-\dfrac{\pi}{6}\right)=16\pi\cos\left(4\pi t-\dfrac{2\pi}{3}+\dfrac{\pi}{2}\right)\) (cm/s), ta suy ra \(\omega=4\pi\left(rad/s\right)\), lại có \(\omega A=16\pi\Leftrightarrow A=\dfrac{16\pi}{\omega}=4\left(cm\right)\)
\(\varphi_0=-\dfrac{2\pi}{3}\); \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)
Đường tròn lượng giác:
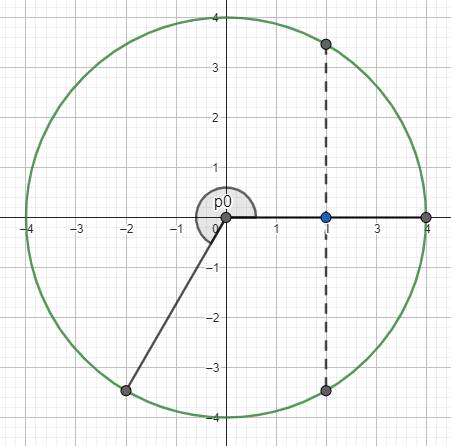
Từ đây, ta có thể thấy tại thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ khi dao động, góc quét của vật là \(\Delta\varphi=\dfrac{\pi}{3}+1011.2\pi=\dfrac{6067}{3}\pi\) (rad)
Thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ lúc bắt đầu dao động là \(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{6067}{3}\pi}{2\pi}.0,5=\dfrac{6067}{12}\approx505,58\left(s\right)\)
Một vật dao động điều hòa dọc theo trục Ox với phương trình x=6cos(10πt+π/3)(cm) . Trong đó t tính bằng giây (s). Tần số dao động của vật là:
A. 0,5 Hz.
B. 0,2 Hz.
C. 5 Hz.
D. 2 Hz.
Một vật dao động điều hòa dọc theo trục Ox với phương trình x =6 cos (4 πt - π /3) cm . Kể từ lúc t = 0 đến khi vật qua vị trí x = ‒3 cm theo chiều âm lần thứ 2017 thì lực kéo về sinh công âm trong khoảng thời gian là
A. 2016,25 s
B. 504,125 s
C. 252,25 s
D. 504,25 s
Một vật dao động điều hòa dọc theo trục Ox với phương trình x = A cos ( ω t + π ) Nếu chọn gốc tọa độ O tại vị trí cân bằng của vật thì gốc thời gian t = 0 là lúc vật.
A. ở vị trí li độ cực đại thuộc phần dương của trục Ox.
B. Qua vị trí cân bằng O ngược chiều dương của trục Ox.
C. ở vị trí li độ cực tiểu thuộc phần âm của trục Ox.
D. Qua vị trí cân bằng O theo chiều dương của trục Ox.
