Gọi M,N lần lượt là điểm biểu diễn hình học các số phức z=2-i và w=4+5i. Tọa độ trung điểm I của đoạn thẳng MN là

A..

B..

C..

D. .

Cho số phức z và w biết w = z 1 - i  và M, N lần lượt là các điểm biểu diễn z, w trong Oxy. Biết diện tích ∆ OMN bằng 1. Tính |z|.

A. |z| = 1 2

B. |z| = 1

C. |z| = 2

D. |z| = 2

Trong mặt phẳng tọa độ Oxy, cho hai điểm M, N lần lượt là các điểm biểu diễn các số phức z 1 = − 4 + i , z 2 = 2 − 9 i . Số phức z 3  có biểu diễn hình học là trung điểm của đoạn thẳng MN. Phát biểu nào sau đây là đúng về số phức z 3 ?

A. z 3 = 1 − 4 i .

B. z 3 = - 1 + 4 i .

C. z 3 = - 1 − 4 i .

D. z 3 = 1 + 4 i .

Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và (1+i)z.

Tính z  biết diện tích tam giác OAB bằng 8.

A.  z = 2 2

B.  z = 4 2

C.  z = 2

D. z = 4

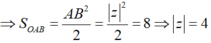
Cho số phức z = 1 + 3 i . Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB.

Cho số phức z = 1 + 3 i . Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB

Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z  và i + 1 z . Tính z biết diện tích tam giác OAB bằng 8.