Viết đa thức x5 + 2x4 – 3x2 – x4 + 1 – x thành: Tổng của hai đa thức

Những câu hỏi liên quan
Viết đa thức x5 + 2x4 – 3x2 – x4 + 1 – x thành: Hiệu của hai đa thức
x5 + 2x4 – 3x2 – x4 + 1 – x = (x5 + 2x4 + 1) – (3x2 + x4 + x)
Đúng 0
Bình luận (0)
Hệ số của
x
4
trong đa thức
Q
(
x
)
5
x
4
-
x
5
-
x
2
-
2
x
3
+
3
x
2
+
3
x
-
2
x
4...
Đọc tiếp
Hệ số của x 4 trong đa thức Q ( x ) = 5 x 4 - x 5 - x 2 - 2 x 3 + 3 x 2 + 3 x - 2 x 4 + 5 là:
A. 2
B. 3
C. 5
D. 1
Thu gọn Q(x) = 5x4 - x5 - x2 - 2x3 + 3x2 + 3x - 2x4 + 5
= -x5 + 3x4 - 2x3 + 2x2 + 3x + 5
Hệ số của x4là 3. Chọn B
Đúng 0
Bình luận (0)
Bài 1. Cho hai đa thức:P(x) 2x4 + 3x3 + 3x2 - x4 - 4x + 2 - 2x2 + 6xQ(x) x4 + 3x2 + 5x - 1 - x2 - 3x + 2 + x3a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảmdần của biến.b) Tính. P(x) + Q (x), P(x) - Q(x), Q(x) - P(x).Bài 2. Cho hai đa thức:P(x) x5 + 5 - 8x4 + 2x3 + x + 5x4 + x2 - 4x3Q(x) (3x5 + x4 - 4x) - ( 4x3 - 7 + 2x4 + 3x5)a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảmdần của biến.b) Tính P(x) + Q(x), P(x) - Q(x)Bài 5. Cho hai đa thức:...
Đọc tiếp
Bài 1. Cho hai đa thức:
P(x) = 2x4 + 3x3 + 3x2 - x4 - 4x + 2 - 2x2 + 6x
Q(x) = x4 + 3x2 + 5x - 1 - x2 - 3x + 2 + x3
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm
dần của biến.
b) Tính. P(x) + Q (x), P(x) - Q(x), Q(x) - P(x).
Bài 2. Cho hai đa thức:
P(x) = x5 + 5 - 8x4 + 2x3 + x + 5x4 + x2 - 4x3
Q(x) = (3x5 + x4 - 4x) - ( 4x3 - 7 + 2x4 + 3x5)
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm
dần của biến.
b) Tính P(x) + Q(x), P(x) - Q(x)
Bài 5. Cho hai đa thức:
P(x) = 2x4 + 2x3 - 3x2 + x +6
Q(x) = x4 - x3 - x2 + 2x + 1
a) Tính P(x) + Q(x), P(x) - Q(x)
b) Tính và P(x) - 2Q(x).
Bài 6. Cho đa thức P(x) = 2x4 - x2 +x - 2.
Tìm các đa thức Q(x), H(x), R(x) sao cho:
a) Q(x) + P(x) = 3x4 + x3 + 2x2 + x + 1
b) P(x) - H(x) = x4 - x3 + x2 - 2
c) R(x) - P(x) = 2x3 + x2 + 1
thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến P(x)=4x5-3x2+3x-2x3-4x5+x4-5x+1+4x2 Q(x)=x7-2x6+2x3-2x4-x7+x5+2x6-x+5+2x4-x5 b)tính p(x)+Q(x);P(x)-Q(x)
a: P(x)=4x^5-4x^5-2x^3+x^4-3x^2+4x^2+3x-5x+1
=x^4-2x^3+x^2-2x+1
Q(x)=x^7-x^7-2x^6+2x^6+2x^3-2x^4+2x^4+x^5-x^5-x+5
=2x^3-x+5
b: P(x)+Q(x)
=x^4-2x^3+x^2-2x+1+2x^3-x+5
=x^4+x^2-3x+6
P(x)-Q(x)
=x^4-2x^3+x^2-2x+1-2x^3+x-5
=x^4-4x^3+x^2-x-4
Đúng 0
Bình luận (0)
Cho đa thức
P
(
x
)
3
x
2
-
3
x
-
1
+
x
4
Q
(
x
)
5
x
3
+
2
x
4
-
x
2
-
5
x
3
-
x
4
+
1
+
3...
Đọc tiếp
Cho đa thức
P ( x ) = 3 x 2 - 3 x - 1 + x 4 Q ( x ) = 5 x 3 + 2 x 4 - x 2 - 5 x 3 - x 4 + 1 + 3 x 2 + 5 x 2
Tìm đa thức R(x) sao cho P ( x ) + R ( x ) = Q ( x )
A. 4 x 2 + 3 x + 2
B. 4 x 2 - 3 x + 2
C. - 4 x 2 + 3 x + 2
D. 4 x 2 + 3 x - 2
Thu gọn Q(x) = x4 + 7x2 + 1
Khi đó R(x) = Q(x) - P(x) = 4x2 + 3x + 2. Chọn A
Đúng 0
Bình luận (0)
Cho các đa thức:
P(x) = x5 – 2x4 + x2 – x + 1
Q(x) = 6 – 2x + 3x3 + x4 – 3x5
Tính P(x) – Q(x) và Q(x) – P(x). Có nhận xét gì về các hệ số của hai đa thức tìm được?
Sắp xếp lại các hạng tử của Q(x) ta có :
Q(x) = –3x5 + x4 + 3x3 – 2x + 6.
Đặt và thực hiện các phép tính P(x) – Q(x) và Q(x) – P(x), ta có
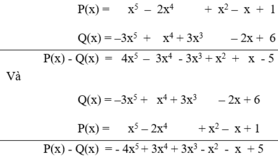
Nhận xét : Các hệ số tương ứng của P(x) – Q(x) và Q(x) - P(x) đối nhau.
Chú ý : Ta gọi hai đa thức có các hệ số tương ứng đối nhau là đa thức đối nhau.
Đúng 1
Bình luận (0)
cho đa thức hai đa thức: P(x)=2x4 + 3x2 - 3x2+6 và Q(x)=x4 + x3 - x2 + 2x +1
A) Tính P(x) + Q(x)
B) Tìm đa thức M(x) biết P (x) + M (x) = 2Q (x)
C) Kiểm tra x= -4 có phải là nghiệm của đa thức M (x) không?
MN giúp mai mik thi r. ko bt làm B, C mong được giúp !!!!
`@` `\text {dnv4510}`
`A)`
`P(x)+Q(x)=`\((2x^4+3x^2-3x^2+6)+(x^4+x^3-x^2+2x+1)\)
`= 2x^4+3x^2-3x^2+6+x^4+x^3-x^2+2x+1`
`= (2x^4+x^4)+x^3+(3x^2-3x^2-x^2)+2x+(6+1)`
`= 3x^4+x^3-x^2+2x+7`
`B)`
`P(x)+M(x)=2Q(x)`
`-> M(x)= 2Q(x) - P(x)`
`2Q(x)=2(x^4+x^3-x^2+2x+1)`
`= 2x^4+2x^3-2x^2+4x+2`
`-> 2Q(x)-P(x)=(2x^4+2x^3-2x^2+4x+2)-(2x^4+3x^2-3x^2+6)`
`= 2x^4+2x^3-2x^2+4x+2-2x^4-3x^2+3x^2-6`
`= (2x^4-2x^4)+2x^3+(-2x^2-3x^2+3x^2)+4x+(2-6)`
`= 2x^3-2x^2+4x-4`
Vậy, `M(x)=2x^3-2x^2+4x-4`
`C)`
Thay `x=-4`
`M(-4)=2*(-4)^3-2*(-4)^2+4*(-4)-4`
`= 2*(-64)-2*16-16-4`
`= -128-32-16-4`
`= -180`
`->` `x=-4` không phải là nghiệm của đa thức.
Đúng 1
Bình luận (1)
Cho hai đa thức: A(x) = 3x3 – 2x2 + x + 1 + x4 và B(x) = 2x4 – x 3 – 5 + 3x2 – 4x a/ Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến. b/ Tính A(x) + B(x) và A(x) – B(x).
a: A(x)=x^4+3x^3-2x^2+x+1
B(x)=2x^4-x^3+3x^2-4x-5
b: A(x)+B(x)
=x^4+3x^3-2x^2+x+1+2x^4-x^3+3x^2-4x-5
=3x^4+2x^3+x^2-3x-4
A(x)-B(x)
=x^4+3x^3-2x^2+x+1-2x^4+x^3-3x^2+4x+5
=-x^4+4x^3-5x^2+5x+6
Đúng 0
Bình luận (0)
Cho đa thức P(x) = 5x3+ 2x4–x2–5x3–x4+ 1 +3x2+ 5x2. Hệ số cao nhất là hệ số tự do của đa thức lần lượt là












