Đường thẳng ∆ nào dưới đây là đường vuông góc chung của d1, d2 với: d 1 : x 4 = y - 1 - 4 = z + 1 - 1 ; d 2 : x + 1 2 = y - 1 1 = z - 3 - 1
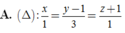
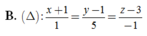
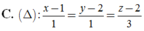
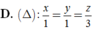
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; 3 và hai đường thẳng d 1 : x − 2 2 = y + 2 − 1 = z − 3 1 và d 2 : x − 1 − 1 = y − 1 2 = z + 1 1 .Gọi ∆ là đường thẳng đi qua A, vuông góc với d 1 và cắt d 2 . Đường thẳng ∆ không nằm trong mặt phẳng nào dưới đây?
A. P 1 : x + 2 y − z − 2 = 0
B. P 2 : 2 x - y + z - 3 = 0
C. P 3 : x - 2 y + 2 z − 1 = 0
D. P 4 : x + 4 y + z − 12 = 0
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d 1 : x - 2 1 = y - 1 - 1 = z - 2 - 1 và d 2 : x = t y = 3 z = - 2 + t . Phương trình đường vuông góc chung của hai đường thẳng d 1 , d 2 là.
A. x = 2 + t y = 1 + 2 t z = 2 - t
B. x = 3 + t y = 3 - 2 t z = 1 - t
C. x = 2 + 3 t y = 1 - 2 t z = 2 - 5 t
D. x = 3 + t y = 3 z = 1 - t
Chọn A.
Gọi d là đường thẳng cần tìm

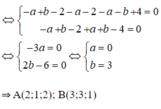
d đi qua điểm A(2;1;2) và có vectơ chỉ phương ![]()

Cho 2 đường thẳng d 1 : x = 2 + t y = 1 - t z = 2 - t và d 2 : x = 3 + t ' y = 2 + t ' z = 5 .Phương trình đường vuông góc chung ∆ của d 1 , d 2 là
A. Δ : x = 1 + t ' ' y = 2 - t ' ' z = 3 + 2 t ' '
B. Δ : x = 1 - t ' ' y = 2 - t ' ' z = 3 + 2 t ' '
C. Δ : x = - 1 + t ' ' y = 2 - t ' ' z = 3 + 2 t ' '
D. Δ : x = 1 + t ' ' y = - 2 - t ' ' z = - 3 + 2 t ' '
Cho hàm số y = f x có đạo hàm tại x = 1 . Gọi d 1 , d 2 lần lượt là tiếp tuyến của đồ thị hàm số y = f x và y = g x = x . f 2 x - 1 tại điểm có hoành độ x = 1 . Biết rằng hai đường thẳng d 1 và d 2 vuông góc với nhau. Khẳng định nào dưới đây đúng
A. 2 < f 1 < 2
B. f 1 ≤ 2
C. f 1 ≥ 2 2
D. 2 ≤ f 1 < 2 2
Chọn đáp án C
Ta có
![]()
Đường thẳng d 1 là tiếp tuyến của đồ thị hàm số y = f x tại điểm x = 1 nên có hệ số góc là k 1 = f ' 1
Đường thẳng d 2 là tiếp tuyến của đồ thị hàm y = g x = x . f 2 x - 1 tại điểm x = 1 nên có hệ số góc là
k 2 = g ' 1 = f 1 + 2 f ' 1
Mà d 1 ⊥ d 2 nên
![]()
![]()
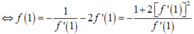
Do f ' 1 ≠ 0 nên
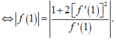
Đặt f ' 1 = t t ≠ 0
Xét hàm số f t = 1 + 2 t 2 t
* Nếu t > 0 thì
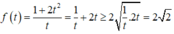
* Nếu t < 0 thì

Vậy h t ≤ 2 2 , ∀ t ≠ 0 hay f 1 ≥ 2 2
Cho hai đường thẳng chéo nhau
d 1 : x − 3 1 = y + 1 − 1 = z − 4 1 và d 2 : x − 2 2 = y − 4 − 1 = z + 3 4 .
Phương trình đường vuông góc chung của d 1 và d 2 là:
A. x − 7 3 = y − 3 2 = z + 9 − 1
B. x − 3 3 = y − 1 2 = z − 1 − 1
C. x − 1 3 = y − 1 2 = z − 2 − 1
D. x + 7 3 = y + 3 2 = z − 9 − 1
Trong không gian Oxyz, cho hai đường thẳng chéo nhau d 1 : x - 1 3 = y + 1 2 = z - 2 - 2 , d 2 : x - 4 2 = y - 4 2 = z + 3 - 1 . Phương trình đường vuông góc chung của hai đường thẳng d 1 , d 2 là
A. x - 4 2 = y + 1 - 1 = z 2
B. x - 2 6 = y - 2 3 = z + 2 - 2
C. x - 2 2 = y - 2 - 1 = z + 2 2
D. x - 4 2 = y - 1 - 1 = z 2
Cho hàm số y=f(x) có đạo hàm tại x=1. Gọi d1,d2 lần lượt là tiếp tuyến của đồ thị hàm số y=f(x) và y=g(x)=x . f(2x-1) tại điểm có hoành độ x=1 Biết rằng hai đường thẳng d1,d2 vuông góc với nhau. Khẳng định nào dưới đây đúng.
A. f ( 1 ) < 2
B. 2 ≤ f ( 1 ) ≤ 2 2
C. 2 ≤ f ( 1 ) ≤ 2
D. f ( 1 ) ≥ 2 2
Trong mặt phẳng tọa độ 0xy , cho hai đường thẳng (d1) : y=1-5tx=4+2t và (d2) : 2x-5y-14=0 . Khẳng định nào sau đây đúng :
a.(d1) (d2) song song với nhau
b. (d1) (d2) vuông góc với nhau
c. (d1) (d2) cắt nhưng không vuông góc với nhau
d. (d1) (d2) trùng nhau
\(\left\{{}\begin{matrix}x=4+2t\\y=1-5t\end{matrix}\right.\)
Vậy: VTCP là (2;-5) và điểm mà (d1) đi qua là A(4;1)
=>VTPT là (5;2)
Phương trình đường thẳng của (d1) là:
5(x-4)+2(y-1)=0
=>5x-20+2y-2=0
=>5x+2y-22=0
(d2): 2x-5y-14=0
=>(d1) và (d2) vuông góc
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y + 2 1 = z - 3 - 1 ; d 2 : x 1 = y - 1 2 = z - 6 3 chéo nhau. Đường vuông góc chung của hai đường thẳng d 1 , d 2 có phương trình là
A. x - 1 5 = y + 2 - 4 = z - 3 1
B. x - 1 5 = y + 1 - 4 = z - 1 1
C. x + 1 5 = y + 1 - 4 = z - 3 1
D. x + 1 3 = y + 1 - 2 = z - 3 1
Đáp án C
![]()
![]()
![]()
Theo giả thiết ta giải hệ điều kiện :
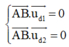
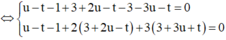
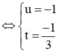
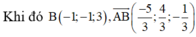
![]()
Vậy PT đường vuông góc chung là AB: x + 1 5 = y + 1 - 4 = z - 3 1