Trong không gian với hệ toạ độ Oxyz, cho điểm A(2;3;4). Khoảng cách từ A đến trục toạ độ Ox bằng
A. 2.
B. 4.
C. 3.
D. 5.
Những câu hỏi liên quan
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;-2;0),B(-2;4;-2). Toạ độ trung điểm của đoạn thẳng AB là
A. (0;2;-2).
B. (0;4;-4).
C. (0;1;-1).
D. (-4;6;-2).
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2;-3;2), B (3;5;4). Tìm toạ độ điểm M trên trục Oz sao cho MA²+MB² đạt giá trị nhỏ nhất.
A. M (0;0;49)
B. M (0;0;67)
C. M (0;0;3)
D. M (0;0;0).
Chọn C
Gọi I là trung điểm của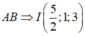 
Ta có: 
IA²+IB² không đổi nên MA²+MB² đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=> M là hình chiếu của I trên trục Oz.
=> M (0;0;3).
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2;-3;2), B (3;5;4). Tìm toạ độ điểm M trên trục Oz so cho MA²+MB² đạt giá trị nhỏ nhất. A. M (0;0;49) B. M (0;0;67) C. M (0;0;3) D. M (0;0;0)
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2;-3;2), B (3;5;4). Tìm toạ độ điểm M trên trục Oz so cho MA²+MB² đạt giá trị nhỏ nhất.
A. M (0;0;49)
B. M (0;0;67)
C. M (0;0;3)
D. M (0;0;0)
Chọn C
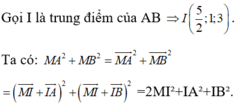
IA²+IB² không đổi nên MA²+MB² đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
Suy ra M là hình chiếu của I trên trục Oz.
Suy ra M (0;0;3).
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho điểm A(2;2;1). Tính độ dài đoạn thẳng OA.
A. OA = 5
B. OA = 3
C. OA = 9
D. OA = 5
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2; -3; 2), B (3; 5; 4). Tìm toạ độ điểm M trên trục ?z sao cho MA2 + MB2 đạt giá trị nhỏ nhất. A. M (0; 0; 49) B. M (0; 0; 67) C. M (0; 0 ;3) D. M (0; 0; 0)
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2; -3; 2), B (3; 5; 4). Tìm toạ độ điểm M trên trục ?z sao cho MA2 + MB2 đạt giá trị nhỏ nhất.
A. M (0; 0; 49)
B. M (0; 0; 67)
C. M (0; 0 ;3)
D. M (0; 0; 0)
Chọn C
Gọi I là trung điểm của AB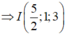 
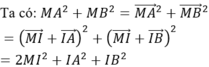
Suy ra: MA2 + MB2 đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=>M là hình chiếu của I trên trục Oz => M (0 ; 0 ; 3)
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2; -3; 2), B (3; 5; 4). Tìm toạ độ điểm M trên trục Oz sao cho
M
A
2
+
M
B
2
đạt giá trị nhỏ nhất. A. M (0; 0; 49). B. M (0; 0; 67) C. M (0; 0 ;3) D. M (0; 0; 0)
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2; -3; 2), B (3; 5; 4). Tìm toạ độ điểm M trên trục Oz sao cho M A 2 + M B 2 đạt giá trị nhỏ nhất.
A. M (0; 0; 49).
B. M (0; 0; 67)
C. M (0; 0 ;3)
D. M (0; 0; 0)
Trong không gian với hệ toạ độ Oxyz, cho điểm M(2;-3;1) và đường thẳng
d
:
x
+
1
2
y
-
2
-
1
z
2
Tìm toạ độ điểm M đối xứng với M qua d A. M’(3;-3;0) B. M’(1;-3;2) C. M...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho điểm M(2;-3;1) và đường thẳng d : x + 1 2 = y - 2 - 1 = z 2 Tìm toạ độ điểm M 'đối xứng với M qua d
A. M’(3;-3;0)
B. M’(1;-3;2)
C. M’(0;-3;3)
D. M’(-1;-2;0)
Đáp án C.
Ta có phương trình mặt phẳng (P) đi qua M và vuông góc với d
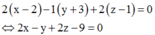
Gọi I là giao điểm của đường thẳng d và (P) khi đó tạo độ I là nghiệm của hệ
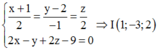
M’ đối xứng với M qua d thì I là trung điểm của MM’ ⇒ M’(0;-3;3)
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho điểm M(2;-3;1) và đường thẳng
d
:
x
+
1
2
y
-
2
-
1
z
2
. Tìm toạ độ điểm M đối xứng với M qua d A. M(3; -3; 0) B. M(1; -3; 2) C. M(0; -3; 3) D. M(-1; -2; 0)
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho điểm M(2;-3;1) và đường thẳng d : x + 1 2 = y - 2 - 1 = z 2 . Tìm toạ độ điểm M 'đối xứng với M qua d
A. M'(3; -3; 0)
B. M'(1; -3; 2)
C. M'(0; -3; 3)
D. M'(-1; -2; 0)
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(3;-2;-2), B(3;2;0), C(0;2;1). Phương trình mặt phẳng (ABC) là: A. 2x -3y +6z 0 B. 4y + 2z -3 0 C. 3x + 2y +1 0 D. 2y + z -3 0
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(3;-2;-2), B(3;2;0), C(0;2;1). Phương trình mặt phẳng (ABC) là:
A. 2x -3y +6z =0
B. 4y + 2z -3 =0
C. 3x + 2y +1 =0
D. 2y + z -3 =0
Đáp án A
(ABC) qua A(3; -2; -2) và có véc tơ pháp tuyến
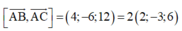
Đúng 0
Bình luận (0)