Cho hình chóp SABC , ΔABC vuông cân tại A , SA ⊥ ABC , BC = a , SBC , ABC = 45 o . Trên tia đối của tia SA lấy điểm R sao cho RS=2SA . Tính VRABC.
A. a 3 12
B. a 3 8
C. a 3 24
D. a 3 4
Cho hình chóp SABC, △ A B C vuông cân tại A, SA ⊥ (ABC), BC=a, ((SBC),(ABC)) = 45 ° . Trên tia đối của tia SA lấy điểm R sao cho RS=2SA. Tính V R A B C .
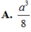
![]()
![]()
![]()
Cho hình chóp SABC, vuông cân tại A, S A ⊥ A B C , B C = a , S B C , A B C = 45 ° . Trên tia đối của tia SA lấy điểm R sao cho R S = 2 S A . Tính V R . A B C .
A. a 3 8
B. a 3 12
C. a 3 4
D. a 3 24
Đáp án A
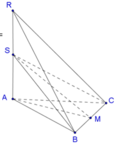
Gọi M là trung điểm của BC. Dễ thấy S M A ^ = 45 °
Tam giác ABC vuông cân tại A suy ra ![]()
Tam giác SAM vuông tại A, S M A ^ = 45 ° suy ra SA = AM = a 2
Vậy 
Mà
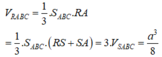
Cho hình chóp SABC có ΔABC vuông cân B, AC=a\(\sqrt{2}\), \(SA\perp\left(ABC\right)\), SA=a
1/ Tính thể tích của khối chóp
2/ Gọi G là trọng tâm ΔABC, mặt phẳng( \(\alpha\)) qua AG // BC \(\cap\) SC, SB lần lượt tại M, N. Tính thể tích khối chóp SAMN
cho hình chóp SABC có SA=a, SA vuông góc với (ABC). Tam giác ABC vuông cân tại B và AB=a, kẻ AH vuông góc với SC tại H. VSABH là
\(\dfrac{V_{SABH}}{V_{SABC}}=\dfrac{SH}{SC}=\left(\dfrac{SA}{SC}\right)^2\Rightarrow V_{SABN}=\left(\dfrac{SA}{SC}\right)^2.V_{SABC}\)
\(AC^2=AB^2+BC^2=2AB^2=2a^2\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{a^2+2a^2}=a\sqrt{3}\)
\(\Rightarrow V_{SABH}=\left(\dfrac{a}{a\sqrt{3}}\right)^2.\dfrac{1}{3}.SA.AB^2=\dfrac{a^3}{9}\)
Cho khối chóp S. ABC , có SA vuông góc với mặt đáy ABC , SA = 2a. Mặt đáy là ΔABC vuông cân tại A, có cạnh BC = 3a. Tính khối chóp S. ABC.
\(AB=AC=\dfrac{BC}{\sqrt{2}}=\dfrac{3a}{\sqrt{2}}\)
\(\Rightarrow V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.2a.\dfrac{1}{2}.\left(\dfrac{3a}{\sqrt{2}}\right)^2=\dfrac{3a^3}{2}\)
Cho hình chóp SABC có đáy là tam giác ABC vuông tại B. SA vuông góc với(ABC), AB = a, AC = 3a, SA = 2a.
a. chứng minh BC vuông góc (ABC).
b. Tính thể tích khối chóp SABC.
Cho hình chóp SABC có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, M là trung điểm BC, J là hình chiếu của A lên BC. Khẳng định nào sau đây đúng ?
A. B C ⊥ S A C
B. B C ⊥ S A M
C. B C ⊥ S A J
D. B C ⊥ S A B
Cho hình chóp SABC có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, M là trung điểm BC, J là hình chiếu của A lên BC. Khẳng định nào sau đây đúng ?
A. BC ⊥ (SAC)
B.BC ⊥ (SAM)
C.BC ⊥ (SAJ)
D. BC ⊥ (SAB)
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B , SA vuông góc với ABC ,SA = a√3 . Xác định và tính góc giữa hai mặt phẳng SBC và ABC
\(SB=\sqrt{\left(a\sqrt{3}\right)^2+a^2}=2a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
(SBC;ABC)=(SB;BA)=góc SBA=60 độ