Trong không gian với hệ tọa độ Oxyz cho mặt phẳng α : 4 x - 3 y - 7 z + 3 = 0 và điểm I(1;-1;2). Phương trình mặt phẳng đối xứng với α qua I là
A. β : 4x - 3y - 7z - 3 = 0
B. β : 4x - 3y - 7z + 11 = 0
C. β : 4x - 3y - 7z - 11 = 0
D. β : 4x - 3y - 7z + 5 = 0
Do β đối xứng với α qua I nên β // α
Suy ra β : 4x - 3y - 7z + D = 0 với D ≠ 3
Chọn 
suy ra tọa độ điểm N đối xứng với M qua I là N(2;-3;2)
Rõ ràng 
nên thay tọa độ vào phương trình
β
ta được D = 11
Vậy phương trình mặt phẳng β : 4x - 3y - 7z + 11 = 0. Chọn B.
Trong không gian Oxyz, cho hai mặt phẳng P : x - 3 y + 2 z - 1 = 0 ; Q : x - z + 2 = 0 . Mặt phẳng α vuông góc với cả (P) và (Q) đồng thời cắt trục Ox tại điểm có hoành độ bằng 3. Phương trình của α là:
A. x + y + z - 3 = 0
B. x + y + z + 3 = 0
C. - 2 x + z + 6 = 0
D. - 2 x + z - 6 = 0
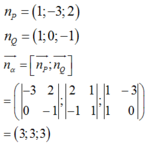
Mp α cắt trục Ox tại điển có hoành độ bằng 3 nên ta có Mp α đi qua điểm M(3,0,0)
ậy phương trình mp α có vtpt n α → 3 , 3 , 3 và đi qua điểm M(3,0,0) có dạng:
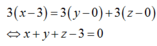
Chọn A.
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0
Tìm điểm M' là ảnh của M(4; 2; 1) qua phép đối xứng qua mặt phẳng (α).
Trong không gian Oxyz, cho hai mặt phẳng P : x - 3 y + 2 z - 1 = 0 , Q : x - z + 2 = 0 . Mặt phẳng α vuông góc với cả (P) và (Q) đồng tời cắt trục Ox tại điểm có hoành độ bằng 3. Phương trình của α là
A. x + y + z - 3 = 0
B. x + y + z + 3 = 0
C. - 2 x + z + 6 = 0
D. - 2 x + z - 6 = 0
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng tiếp xúc với (S): x 2 + y 2 + z 2 - 2 z - 4 y - 6 z - 2 = 0 và song song với (α): 4x + 3y - 12z+10 = 0
A.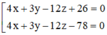 
B.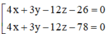 
C.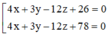 
D.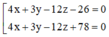 
Đáp án D
Phương pháp:
(P) // (α) => Phương trình mặt phẳng (P) có dạng 4x + 3y - 12z + D = 0 (D ≠ 0)
(P) tiếp xúc với (S) => d(I;(P)) = R với I; R là tâm và bán kính mặt cầu (S)
Cách giải:
Gọi mặt phẳng (P) là mặt phẳng cần tìm
(P) // (α) Phương trình mặt phẳng (P) có dạng 4x + 3y - 12z + D = 0 (D ≠ 0)
Mặt cầu (S) có tâm I (1;2;3), bán kính R = 4
(P) tiếp xúc với (S) => d(I;(P)) = R
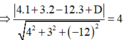
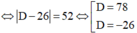
Vậy mặt phẳng (P) thỏa mãn yêu cầu bài toán có phương trình
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0 Chứng minh rằng (α) cắt ( β)
Trong không gian Oxyz, cho điểm A(–1;3; –2) và mặt phẳng (α): x – 2y – 2z + 5 = 0. Khoảng cách từ điểm A đến mặt phẳng (α) bằng:
A. 1
B. 2 3
C. 2 9
D. 2 5 5
Đáp án B
Phương pháp: Xét M(x0;y0;z0), (α): Ax+By+Cz+D = 0
Khoảng cách từ M đến (α) là: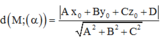 
Cách giải: Khoảng cách từ A đến (α) là: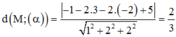 
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0
Viết phương trình tham số của đường thẳng d là giao của (α) và ( β)
Trong không gian Oxyz, cho hai mặt phẳng α :2x+y-2z+1=0; β :x-2y+2z+3=0 Tập hợp tất cả các điểm trong không gian cách đều hai mặt phẳng đã cho là
A. Một mặt phẳng duy nhất
B. Một điểm duy nhất
C. Hai mặt phẳng phân biệt vuông góc với nhau
D. Một đường thẳng duy nhất song song với cả hai mặt phẳng đã cho
Điểm cần tìm M(x;y;z) ta có điều kiện cách đều hai mặt phẳng là
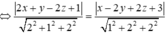
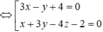
Vậy tập hợp các điểm này nằm trên hai mặt phẳng vuông góc với nhau (hai mặt phẳng này được gọi là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng).
Chọn đáp án C.
Chọn đáp án C.
