Gọi S là tập hợp các số thực m sao cho với mỗi m ∈ S có đúng một số phức thỏa mãn z - m = 4 và z z - 6 là số thuần ảo. Tính tổng của các phần tử của tập S.
A. 0
B. 12
C. 6
D. 14
Gọi S là tập hợp các số thực m sao cho với mỗi m ∈ S có đúng một số phức thỏa mãn z - m = 6 và z z - 4 là số thuần ảo. Tính tổng của các phần tử của tập S.
A. 10
B. 0
C. 16
D. 8
Đáp án B
Phương pháp.
Gọi ![]() . Sử dụng giả thiết để tìm a, bsuy ra giá trị của z. Sử dụng kết quả này để tìm giá trị của m và kết luận.
. Sử dụng giả thiết để tìm a, bsuy ra giá trị của z. Sử dụng kết quả này để tìm giá trị của m và kết luận.
Lời giải chi tiết.
Giả sử ![]() Khi đó ta có
Khi đó ta có
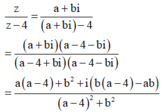
Để ![]() là số thuần ảo thì ta phải có
là số thuần ảo thì ta phải có
![]()
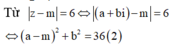
Từ (1) suy ra ![]() thay vào (2) ta nhận được
thay vào (2) ta nhận được
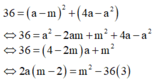
Nếu m=2 thì (3) vô nghiệm
Nếu m
≠
2 thì từ (3) suy ra ![]()
Vì ![]() nên để có duy nhất một số phức z thỏa mãn điều kiện đã cho thì b=0
nên để có duy nhất một số phức z thỏa mãn điều kiện đã cho thì b=0
Ta nhận được a=0 hoặc a=4
với a=4 thì z=a+bi=4. Loại vì ![]() là số thuần ảo
là số thuần ảo
vậy a=b=0
⇒
z=0. Khi đó ![]()
Tổng các phần tử của S là 6+(-6)=0
Gọi S là tập hợp các số thực m sao cho với mỗi m ∈ S có đúng một số phức thỏa mãn z - m = 6 v à z z - 4 là số thuần ảo. Tính tổng của các phần tử của tập S
![]()
![]()
![]()
![]()
Gọi S là tập hợp các số thực m sao cho với mỗi m ∈ S có đúng một số phức thỏa mãn | z - m | = 6 v à z z - 4 là số thuần ảo. Tính tổng của các phần tử của tập S.
A. 10
B. 0
C. 16
D. 8
Gọi S là tập hợp các số thực m sao cho với mỗi m ∈ S có đúng một số phức thỏa mãn z - m = 4 và z z - 6 là số thuần ảo. Tính tổng của các phần tử của tập S
A. 0
B. 12.
C. 6
D. 14
Gọi S là tập hợp giá trị thực của tham số m sao cho phương trình z 2 - m + 4 z + m 2 + 3 = 0 có nghiệm phức z 0 thỏa mãn z 0 = 2 . Số phần tử của tập hợp S là
A. 4
B. 3
C. 2
D. 1
Gọi S là tập hợp các số nguyên m sao cho tồn tại 2 số phức phân biệt z 1 , z 2 thỏa mãn đồng thời các phương trình z - 1 = z - i và z + 2 m = m + 1 . Tổng các phần tử của S là
A. 1
B. 4
C. 2
D. 3
Gọi S là tập hợp tất cả các giá trị thực của m để tồn tại 4 số phức z thỏa mãn | z + z ¯ | + | z - z ¯ | = 2 và z ( z ¯ + 2 ) - ( z + z ¯ ) - m là số thuần ảo. Tổng các phần tử của S là:
A. c
B. 2 + 1 2
C. 2 - 1 2
D. 1 2
Gọi S là tập hợp các số thực m sao cho với mỗi m € S có đúng một số phức thỏa mãn | z-m|= 6 và z: z-4 là số thuần ảo. Tính tổng của các phần tử của S
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn đồng thời các phương trình z - 1 = z - i và z + 2 m = m + 1 . Tổng tất cả các phần tử của S là
![]()
![]()
![]()
![]()