Trong không gian Oxyz, cho vectơ O A → = j → - 2 k → . Tọa độ điểm A là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho vectơ a → = 2 i → - j → - 2 k → . Độ dài của vectơ a → bằng
A. 5
B. 9
C. 5
D. 3
Trong không gian Oxyz, cho vectơ a → = 2 i → + k → - 3 j → Tìm tọa độ của vectơ a →
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ O ; i → ; j → ; k → , cho hai vectơ a → = 2 ; - 1 ; 4 và b → = i → - 3 k → . Tính a → . b →
A. -10
B. -13
C. 5
D. -11
Trong không gian Oxyz, cho vectơ O M → = - j → + 5 k → . Khi đó tọa độ điểm M là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho điểm A thỏa mãn OA → = 2 i → + j → là hai vectơ đơn vị trên hai trục tọa độ Ox, Oy. Tọa độ điểm A là:
A . A ( 2 ; 1 ; 0 )
B . A ( 0 ; 2 ; 1 )
C . A ( 0 ; 1 ; 1 )
D . A ( 1 ; 1 ; 1 )
Trong không gian Oxyz, cho vectơ a → = (-1; -2; 3). Tìm tọa độ của vectơ b → = (2; y; z) biết rằng vectơ b → cùng phương với vectơ a →
A. b → = 2 ; - 2 ; 3
B. b → = 2 ; 4 ; 6
C. b → = 2 ; - 4 ; 6
D. b → = 2 ; 4 ; - 6
Đáp án D
Vectơ b → cùng phương với vectơ a → khi và chỉ khi tồn tại một số thực k thỏa mãn:
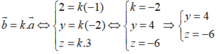
Trong không gian Oxyz, cho vectơ a → = (1; -2; 3). Tìm tọa độ của vectơ b → biết rằng vectơ b → ngược hướng với vectơ a → và | b → | = 2| a → |
A. b → = 2 ; - 4 ; 6 B. b → = 2 ; - 2 ; 3 C. b → = - 2 ; 4 ; - 6 b → = - 2 ; - 2 ; 3 D.
B. b → = 2 ; - 2 ; 3
C. b → = - 2 ; 4 ; - 6
D. b → = - 2 ; - 2 ; 3
Đáp án C
Vì vectơ b → ngược hướng với vectơ a → và | b → | = 2| a → | nên:
b → = -2 a → = (-2; 4; -6)
Trong không gian Oxyz , cho vectơ a ⇀ = (2; 1; -2). Tìm tọa độ của các vectơ b ⇀ cùng phương với vectơ a ⇀ và có độ dài bằng 6.
A. b ⇀ = 4 ; 2 ; - 4
B. b ⇀ = - 4 ; - 2 ; 4
C. b ⇀ = 4 ; 2 ; - 4 hoặc b ⇀ = - 4 ; - 2 ; 4
D. b ⇀ = 12 ; 6 ; - 12 hoặc b ⇀ = - 12 ; - 6 ; 12
Đáp án C
Ta có:
![]()
Mặt khác hai vectơ này cùng phương nên ta có:
![]()
Từ đó ta suy ra
![]()
Lưu ý. Đáp án D là sai, do sai lầm trong tính độ dài của vectơ a ⇀
![]()
Mà hai vectơ này cùng phương nên ta có:
![]()
Trong không gian Oxyz, cho hai điểm A(1;1;0), B(2;-1;1). Một vectơ pháp tuyến n → của mặt phẳng (OAB) (Với O là gốc tọa độ) là
A. (-3;1;-1)
B. (1;-1;-3)
C. (1;-1;3)
D. (1;1;3)