Có bao nhiêu số thực α thuộc π ; 3 π thỏa mãn ∫ π α cos 2 x d x = 1 4
A. 6
B. 5
C. 4
D. 3
Những câu hỏi liên quan
Có bao nhiêu số thực α thuộc ( π , 3 π ) thỏa mãn ∫ π α c o s 2 x d x = 1 4
A. 6
B. 5
C. 4
D. 3
Có bao nhiêu số thực a thuộc
(
π
;
3
π
)
thỏa mãn
∫
π
a
cos
2
x
d
x
1
4
.
Đọc tiếp
Có bao nhiêu số thực a thuộc ( π ; 3 π ) thỏa mãn ∫ π a cos 2 x d x = 1 4 .
Có bao nhiêu số thực b thuộc khoảng
π
,
3
π
sao cho
∫
π
b
4
cos
2
x
d
x
1
A. 8. B. 2. C. 4. D. 6.
Đọc tiếp
Có bao nhiêu số thực b thuộc khoảng π , 3 π sao cho ∫ π b 4 cos 2 x d x = 1
A. 8.
B. 2.
C. 4.
D. 6.
Chọn C
Ta có
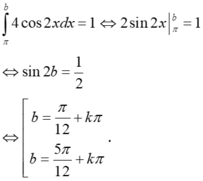
Do đó, có 4 số thực b thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Có bao nhiêu số thực b thuộc
π
;
3
π
sao cho
∫
a
b
4
cos
2
x
d
x
1
A. 0 B. 2 C. 4 D. 6
Đọc tiếp
Có bao nhiêu số thực b thuộc π ; 3 π sao cho ∫ a b 4 cos 2 x d x = 1
A. 0
B. 2
C. 4
D. 6
Có bao nhiêu số thực b thuộc
π
;
3
π
sao cho
∫
π
b
4
c
os
2
x
d
x
1
?
A. 8 B. 2 C. 4 D. 6
Đọc tiếp
Có bao nhiêu số thực b thuộc π ; 3 π sao cho ∫ π b 4 c os 2 x d x = 1 ?
A. 8
B. 2
C. 4
D. 6
Đáp án C
Ta có ∫ π b 4 c os 2 x d x = 2 sin 2 x π b = 2 ⇔ sin 2 b = 1 sin 2 b = 1 2 ⇔ b = π 12 + k π b = 5 π 12 + k π k ∈ ℤ
b ∈ π ; 3 π ⇒ π < π 12 + k 1 π < 3 π π < 5 π 12 + k 2 π < 3 π ⇔ 11 12 < k 1 < 35 12 7 12 < k 2 < 31 12 ⇒ k 1 1 ; 2 k 2 1 ; 2
Suy ra có 4 giá trị thực của b thuộc π ; 3 π thỏa mãn đề bài.
Đúng 0
Bình luận (0)
Có bao nhiêu số thực a thuộc π ; 3 π thỏa mãn ∫ π a cos 2 x d x = 1 4
A. 6.
B. 5.
C. 4.
D. 3.
Cho hình vuông có O là tâm. Có bao nhiêu phép quay tâm O góc α ( 0 ≤ α ≤ π ) biến hình vuông trên thành chính nó?
A.1
B.2
C.3
D.4
Đáp án C
Phép quay tâm O góc quay k. 90 o biến hình vuông thành chính nó.
Đúng 0
Bình luận (0)
Cho tam giác đều có O là tâm. Có bao nhiêu phép quay tâm O góc α ( 0 ≤ α ≤ π ) biến tam giác trên thành chính nó?
A.1
B.2
C.3
D.4
Đáp án B
Phép quay tâm O góc quay k. 120 o biến tam giác đều thành chính nó
Đúng 0
Bình luận (0)
Phương trình (sinx - cosx)(sinx + 2cosx - 3) 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng
-
3
π
4
;
π
? A. 3 B. 0. C. 1. D. 2.
Đọc tiếp
Phương trình (sinx - cosx)(sinx + 2cosx - 3) = 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng - 3 π 4 ; π ?
A. 3
B. 0.
C. 1.
D. 2.
