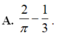
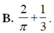
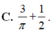
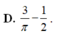
Tính diện tích hình phẳng giới hạn bởi y = x + 1 2 và 0 ≤ y ≤ 1
A. 2 π - 1 3
B. 2 π + 1 3
C. 3 π + 1 2
D. 3 π - 1 2
Ta có
x = sin πy ∈ - 1 ; 1 ⇒ x + 1 ≥ 0
Mà 0 ≤ y ≤ 1 nên y = x + 1 2 ⇔ x = y - 1
Vậy S = ∫ 0 1 sin πy - y + 1 d y = 2 π + 1 3
Đáp án B
Tính diện tích hình phẳng giới hạn bởi các đường sau: x + y = 1, x + y = -1, x – y = 1, x – y = -1
Tính diện tích hình phẳng giới hạn bởi các đường y = x 2 + x - 1 và y = x 4 + x - 1 là:
A. 4 15
B. 15 4
C. 4,15
D. 4,05
Phương trình hoành độ giao điểm của hai đường cong là
x 2 + x - 1 = x 4 + x - 1 ⇔ x 2 - x 4 = 0 ⇔ x ∈ 0 ; 1 ; - 1
Khi đó diện tích cần tìm là
S = ∫ - 1 1 x 2 - x 4 d x = ∫ - 1 0 x 2 - x 4 d x + ∫ 0 1 x 2 - x 4 d x = x 3 3 - x 5 5 - 1 0 + x 3 3 - x 5 5 0 1 = 4 15
Đáp án A
Tính diện tích S của hình phẳng giới hạn bởi các đường y = e x , y = e - x , x = 1 .
A. S = e + 1 2 - 2
B. S = e - 1 e - 2
C. S = e + 1 e
D. S = e + 1 e - 2
Tính diện tích S của hình phẳng giới hạn bởi các đường y = ex, y = e–x, x = 1.
A. S = e + 1 2 - 2
B. S = e - 1 e - 2
C. S = e + 1 e
D. S = e + 1 e - 2
Tính diện tích hình phẳng giới hạn bởi:
y = x , y = x - 2 , y = 0
A. 3
B. 10
C. 10 3
D. 3 10
Tính diện tích hình phẳng giới hạn bởi: y = x , y = x - 2 , y = 0
A. 3
B. 10
C. 10 3
D. 3 10
Tính diện tích S của hình phẳng giới hạn bởi các đường y = e x , y = 2 , x = 0 , x = 1 .
A. S = 4 ln 2 + e - 5
B. S = 4 ln 2 + e - 6
C. S = e 2 - 7
D. S = e - 3
Tính diện tích các hình phẳng giới hạn bởi các đường sau: y = x - 1 + lnx x , y = x - 1 và x = e
