Mặt phẳng chứa trục Ox và chứa điểm M(4;-1;2) có phương trình
Những câu hỏi liên quan
Mặt phẳng chứa trục Ox và chứa điểm M(4;-1;2) có phương trình
A. 2y + z = 0.
B. 4x + 3y = 0.
C. 3x + z = 0.
D. 2y – z = 0.
Viết phương trình mặt phẳng chứa trục Ox và chứa điểm M(4; -1; 2)
A. 2y + z = 0
B. 4x + 3y = 0
C. 3x + z = 0
D. 2y – z = 0
Lập phương trình mặt phẳng: Chứa trục Ox và điểm P(4; -1; 2)
(P) chứa Ox và điểm P(4; -1; 2).
+ (P) chứa Ox ⇒ nhận i → = (1; 0; 0) là 1 vtcp
+ (P) chứa O(0 ; 0 ; 0) và P(4 ; -1 ; 2) ⇒ nhận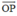 
= ( 4 ; -1 ; 2) là 1 vtcp
⇒ (P) nhận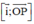 
= (0; -2; -1) là 1 vtpt
⇒ (P): -2.(y – 0) – 1.(z – 0) = 0
hay (P) : 2y + z = 0.
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, mặt phẳng qua điểm M(1;2;3) và chứa trục Ox là
A. x-1=0.
B. 2y+3z-13=0.
C. 3y-2z=0.
D. 2y-3z=0.
Trong không gian Oxyz, cho điểm M(1;0;-1). Mặt phẳng ( α ) đi qua M và chứa trục Ox có phương trình là
A. x+y+z=0
B. y+z+1=0
C. y=0
D. x+z=0
Trong không gian Oxyz, cho điểm M(1;0;-1). Mặt phẳng (α) đi qua M và chứa trục Ox có phương trình là?
A. x+z = 0
B. y+z+1 = 0
C. y = 0
D. x+y+z = 0
Trong không gian Oxyz, cho điểm M(1;0;-1). Mặt phẳng α đi qua M và chứa trục Ox có phương trình là
A. x + z = 0
B. y + z + 1 = 0
C. y = 0
D. x + y + z = 0
Trong không gian Oxyz, cho điểm M(1;0;-1). Mặt phẳng
(
α
)
đi qua M và chứa trục Ox có phương trình là A. x + z 0 B. y + z +1 0 C. y 0 D. x + y + z 0
Đọc tiếp
Trong không gian Oxyz, cho điểm M(1;0;-1). Mặt phẳng ( α ) đi qua M và chứa trục Ox có phương trình là
A. x + z = 0
B. y + z +1 = 0
C. y = 0
D. x + y + z = 0
Đáp án C
Phương pháp:
+) Phương trình đường thẳng đi điểm M ( x 0 ; y 0 ; z 0 ) và có VTPT n → = ( a ; b ; c ) có phương trình:
+) Hai vecto u → , v → cùng thuộc một mặt phẳng thì mặt phẳng đó có VTPT là: n → = u → , v →
Cách giải:
Mặt phẳng ( α ) chứa điểm M và trục Ox nên nhận n α → = O M → , u O x → là một VTPT.
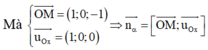
Kết hợp với ( α ) đi qua điểm M(1;0;-1)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng chứa trục Ox và điểm P(4;-1;2) là:
A. 2x+z=0
B. 2x+y=0
C. 2y+z=0
D. 2x+y+z=0
