Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của P = z + i z với z là số phức khác 0 và thỏa mãn z ≥ 2 Tính giá trị của 2M – m.
A. 2M – m =3/2
B. 2M – m =5/2
C. 2M – m =10
D. 2M – m =6
Cho số phức z thỏa mãn z + 2 − i + z − 5 + 6 i = 7 2 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = z − 1 + 2 i . Tổng M + m là:
A. 2
B. 3 2 .
C. 4 2 .
D. 7 2 .
Đáp án C
Đặt z = x + yi , ( x ; y ∈ ℝ ) . Số phức z được biểu diễn bởi điểm N(x;y)
Số phức z 1 = − 2 + i được biểu diễn bởi điểm A(-2;1)
Số phức z 2 = 5 − 6 i được biểu diễn bởi điểm B(5;-6)
Ta có: z + 2 − i + z − 5 + 6 i = 7 2 ⇔ NA + NB = 7 2 . Mà AB = 7 2 nên N thuộc đoạn thẳng AB.
Đường thẳng AB : qua A − 2 ; 1 qua B 5 ; − 6 => phương trình đường thẳng AB là: x + y +1 = 0.
Vì N(x;y) thuộc đoạn thẳng AB nên x + y +1 = 0, x∈ − 2 ; 5 .
Ta có:
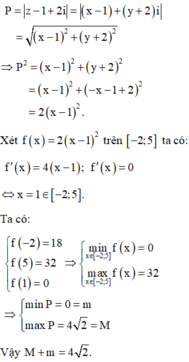
Cho số phức z thỏa mãn |z + 2 - i| + |z - 5 + 6i| = 7 2 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = |z - 1 + 2i|. Tổng M + m là:
A. 2.
B. 3 2
C. 4 2
D. 7 2
Đáp án C
Đặt ![]() Số phức z được biểu diễn bởi điểm N(x;y)
Số phức z được biểu diễn bởi điểm N(x;y)
Số phức ![]() được biểu diễn bởi điểm A(-2;1)
được biểu diễn bởi điểm A(-2;1)
Số phức ![]() được biểu diễn bởi điểm B(5;-6)
được biểu diễn bởi điểm B(5;-6)
được biểu diễn bởi điểm
Ta có: |z + 2 - i| + |z - 5 + 6i| = 7
2
![]() Mà AB = 7
2
nên N thuộc đoạn thẳng AB.
Mà AB = 7
2
nên N thuộc đoạn thẳng AB.
Đường thẳng AB: 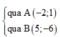
=> phương trình đường thẳng AB là: x + y + 1 = 0
Vì N(x;y) thuộc đoạn thẳng AB nên x + y +1 = 0, x ∈ [-2;5]
Ta có: ![]()
![]()
![]()
![]()
Xét ![]() trên [-2;5] ta có: f'(x) = 4(x-1)
trên [-2;5] ta có: f'(x) = 4(x-1)
![]()
Ta có:
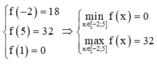
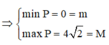
Vậy M + m = 4 2
Xét các số phức z thỏa mãn thiết | z + 2 - i| + | z - 4 - 7i|= 6 2 . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của |z – 1 + i|. Tính P = m + M.
![]()
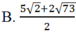
![]()
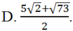
Chọn B.
Ta có: ![]()
Suy ra: ![]()
Xét điểm A(-2; 1) và B(4; 7) , phương trình đường thẳng AB: x - y + 3 = 0.
Gọi M(x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Khi đó ta có ![]() và ta thấy
và ta thấy ![]() , suy ra quỹ tích M thuộc đoạn thẳng AB.
, suy ra quỹ tích M thuộc đoạn thẳng AB.
Xét điểm C( 1; -1); ta có ![]() , hình chiếu H của C trên đường thẳng AB nằm trên đoạn AB.
, hình chiếu H của C trên đường thẳng AB nằm trên đoạn AB.
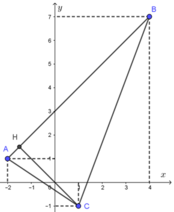
Do đó 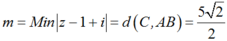
![]()
Vậy 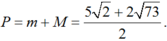
Cho số phức z thoả mãn | z 2 + 16 | + | z ( z + 4 i ) | = 4 | z + 4 i | . Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z+1-i|. Tính P=M+m.
A. P = 26 + 10
B. P = 1 + 10
C. P = 2 + 26
D. P = 26 + 1
Cho số phức z thỏa mãn | ( z + 2 ) i + 1 | + | ( z ¯ - 2 ) i - 1 | = 10 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z|. Tính tổng S=M+m.
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn: |z+2+i| = 4. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z-1-2i|. Tính S = M + m.
A. 6 2
B. 4 2
C. 2 2
D. 8 2
Cho số phức z thỏa mãn: z + 2 + i = 4 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z − 1 − 2 i . Tính S = M + m.
A. 6 2
B. 4 2
C. 2 2
D. 8 2
Đáp án A
Em có:
4 = z + 2 + i = z − 1 − 2 i + 3 + 3 i ≥ z − 1 − 2 i − 3 + 3 i
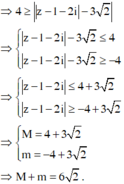
Xét các số phức z thỏa mãn điều kiện z − 3 + 4 i + z + 2 − i = 5 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z − 4 − 3 i . Tính tổng bình phương của M và m.
A. 82
B. 162
C. 90
D. 90 + 40 5
Xét các số phức z thỏa mãn điều kiện z − 3 + 4 i + z + 2 − i = 5 2 . Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z − 4 − 3 i . Tính tổng bình phương của M và m.
A. 82
B. 162
C. 90
D. 90 + 40 5
Đáp án A.
Giả sử z = a + b i , a , b ∈ ℝ . Khi đó
z − 3 + 4 i + z + 2 − i = 5 2 ⇔ a − 3 2 + b + 4 2 + a + 2 2 + b − 1 2 = 5 2
Coi I a ; b , P 3 ; − 4 , Q − 2 ; 1 và R 4 ; 3 , với chú ý P Q = 5 2 thì đẳng thức trên trở thành I P + I Q = P Q .
Đẳng thức trên chỉ xảy ra khi I thuộc đoạn PQ. Hơn nữa z − 4 − 3 i = I R .
Nhận thấy tam giác PQR là tam giác có ba góc nhọn nên
min R I = d R , P Q ; max R I = max R P , R Q
Bằng tính toán ta có m = 4 2 ; M = 5 2 . Suy ra M 2 + m 2 = 82 .
Cho số phức z thỏa mãn điều kiện z - 1 - 2 i = 4 Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z + 2 + i Tính giá trị của tổng S=M2+ m2
A. S = 82
B. . S = 34
C. S = 68
D. S = 36.