Cho dãy số (un) thỏa mãn log u 1 + 2 + log u 1 - 2 log u 10 = 2 log u 10 và un+1 = 2un với mọi n ≥ 1 . Giá trị nhỏ nhất của n để un > 5100 bằng
A. 247.
B. 248.
C. 229.
D. 290.
Cho dãy số (un) thỏa mãn log u 1 + - 2 + log u 1 - 2 log u 8 = 2 log u 10 và un+1 = 10un, ∀ n ∈ R* Khi đó u2018bằng
A. 102000
B. 102008
C. 101008
D. 102017
Chọn A.
Dễ thấy un là cấp số nhân với q = 10
Ta có: u8 = 107u1; u10 = 109u1
Do đó PT ![]()
![]()
![]()
Giải PT ta được logu1 = -17 ⇔ u1 = 10-17 ⇒ u2018 = 102017 u1 = 102000
Cho dãy số ( u n ) thỏa mãn log u 1 + 2 + log u 1 - 2 log u 10 = 2 log u 10
và u n + 1 = 2 u n với mọi n ≥ 1 Giá trị nhỏ nhất của n đề u n > 5 100 bằng
A. 247
B. 248
C. 229
D. 290
Cho dãy số
(
u
n
)
gồm 89 số hạng thỏa mãn ![]() Gọi P là tích của tất cả 89 số hạng của dãy số. Giá trị của biểu thức log P là
Gọi P là tích của tất cả 89 số hạng của dãy số. Giá trị của biểu thức log P là
A. 89
B. 1
C. 0
D. 10
Đáp án C
Phương pháp : Áp dụng công thức :
tanα.cotα = 1ó tanα(tan900 – α) = 1
Cách giải : Ta có : ![]() >P = tan10.tan20.tan30…tan890
>P = tan10.tan20.tan30…tan890
óP=(tan10.tan890).(tan20.tan880).(tan30.tan870)…tan450
óP=(tan10.cot10).(tan20.cot20).(tan30.cot30)…..(tan440.cot440).tan450
óP=1.1.1…..1=1 =>logP = log1 = 0
Cho a,b là các số thực thỏa mãn log 2 . log 2 a - log b = 2 . Hỏi a,b thỏa mãn hệ thức nào dưới đây?
A. a = 100b
B. a = 100 - b
C. a = =100 + b
D. a = 100 b
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0.
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Cho a là số nguyên dương lớn nhất thỏa mãn \(3{\log _3}\left( {1 + \sqrt a + \sqrt[3]{a}} \right) > 2{\log _2}\sqrt a\).Tìm phần nguyên của \({\log _2}\left( {2017a} \right)\)
A.14
B.22
C.16
D.19
Cho các số thực x, y, z thỏa mãn y = 10 1 1 - log x , z = 10 1 1 - log y . Mệnh đề nào sau đây đúng?
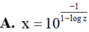
![]()
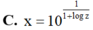
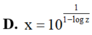
Đáp án D
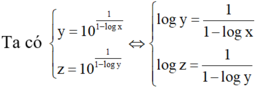
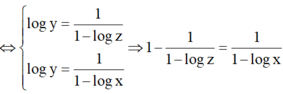
⇔ log z - 1 log z = 1 1 - log x
⇔ 1 - log x = log z log z - 1
⇔ log x = - 1 log z - 1 ⇔ x = 10 1 1 - log z .
Cho hai số thực dương x, y thỏa mãn log x + log y ≥ log ( x 3 + 2 y ) Giá trị nhỏ nhất của P = 25x + y là
A. 375/4
B. 45/2
C. 195/2
D. 14 26