Cho f(x) là hàm số liên tục thỏa ∫ 0 1 f ( x ) d x = 7 Tính ∫ 0 π 2 cos x f ( sin x ) d x
A. 1
B. 9
C. 3
D. 7
Cho f(x) là hàm số liên tục trên R thỏa mãn f(x) + f'(x) = x và f(0) = 1. Tính f(1).
A. 2/e
B. 1 / e
C. e
D. e / 2
Chọn A
![]() .
.
Nhân 2 vế của ![]() với
với ![]() ta được
ta được ![]() .
.
Hay ![]() .
.
Xét ![]() .
.
Đặt ![]() .
.
![]()
Suy ra ![]() .
.
Theo giả thiết ![]() nên
nên ![]()
![]() .
.
Cho hàm số f(x)có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(1)=0; ∫ 0 1 [ f ' ( x ) ] 2 d x = 7 và ∫ 0 1 x 2 f ( x ) d x = 1 3 .Tích phân ∫ 0 1 f ( x ) d x bằng
A. 7/5
B. 1
C. 7/4
D. 4
Cho f(x) là hàm số liên tục trên R thỏa mãn f(x) + f'(x) = sinx với mọi x và f(0) = 1. Tính e x f ( π ) .
A. e x - 1 2
B. e x + 1 2
C. e x + 3 2
D. π + 1 2
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(1) = 0 ∫ 0 1 f ' ( x ) 2 d x = 7 , ∫ 0 1 x 2 f ( x ) d x = 1 3 Tích phân ∫ 0 1 f ( x ) d x bằng:
A. 7/5
B. 1
C. 7/4
D. 4
Cho hàm số f (x) có đạo hàm liên tục trên đoạn [1;2] thỏa mãn ∫ 1 2 ( x - 1 ) 2 f ( x ) d x = - 1 3 , f(2) = 0 và ∫ 1 2 f ' ( x ) 2 d x = 7 . Tính tích phân ∫ 1 2 f ( x ) d x
A. I = 7 5
B. I = - 7 5
C. I = - 7 20
D. I = 7 20
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(1)=0, ∫ 0 1 f ' ( x ) 2 d x = 7 và ∫ 0 1 x 2 f x d x = 1 3 . Tích phân ∫ 0 1 f ( x ) d x bằng
A. 7 5
B. 1
C. 7 4
D. 4
Đáp án A.
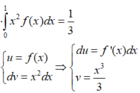
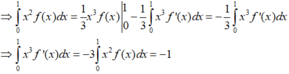
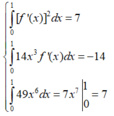
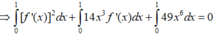

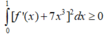
Nên đẳng thức xảy ra khi và chỉ khi
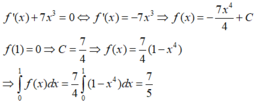
Cho hàm số y = f (x) thỏa mãn f(0) = 1, f'(x) liên tục trên R và ∫ 0 3 f ' ( x ) dx = 9 .Giá trị của f(3) là
A. 6
B. 3
C. 10
D. 9
Cho hàm số y = f (x) thỏa mãn f(0) = 1, f'(x) liên tục trên R và ∫ 0 3 f ' ( x ) d x = 9 . Giá trị của f(3) là
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ thỏa mãn f'(x) -xf(x) = 0, f x > 0 , ∀ x ∈ ℝ và f(0) = 1. Giá trị của f(1) bằng?
A. 1 e .
B. 1 e .
C. e .
D. e.
Cho hàm số y=f (x) liên tục trên R thỏa mãn l i m x → - ∞ f ( x ) = 0 ; l i m x → + ∞ f ( x ) = 1 . Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số đã cho là:
A. 2
B. 1
C. 3
D. 0
Đáp án A
Phương pháp:
Nếu l i m x → + ∞ y = a hoặc l i m x → - ∞ y = a thì y = a là TCN của đồ thị hàm số y = f(x)
Nếu l i m x → b + y = ∞ hoặc l i m x → b - y = ∞ thì x = b là TCĐ của đồ thị hàm số y = f(x)
Cách giải: Do hàm số liên tục trên R nên đồ thị hàm số không có TCĐ.
l i m x → - ∞ f ( x ) = 0 ; l i m x → + ∞ f ( x ) = 1 → y = 0 và y = 1 là 2 đường TCN của đồ thị hàm số.