Cho số phức z thỏa mãn: |z-3-4i| = 1. Tìm giá trị lớn nhất của |z|
A. 4
B. 5
C. 6
D. 7
Cho số phức z thỏa mãn: z − 3 − 4 i = 1 . Tìm giá trị lớn nhất của z
A. 4
B. 5
C. 6
D. 7
Đáp án C
Em có: z = z − 3 − 4 i + 3 + 4 i ≤ z − 3 − 4 i + 3 + 4 i
=> z ≤ 1 + 5 = 6
=> Giá trị lớn nhất của |z| là 6
Cho các số phức z thỏa mãn |z|=2và w=1- 3 i+(3-4i)z. Tìm giá trị lớn nhất của |w|
A. 8.
B. 9.
C.10.
D. 12.
Cho số phức z thỏa mãn z - 3 + 4 i = 4 . Giá trị lớn nhất của z 2 là
A. 44
B. 65
C. 81
D. 100
Cho số phức z thỏa mãn | z -3 - 4i| = 5 .Tìm |z| để biểu thức: P = |z + 2|2 - |z – i|2 đạt giá trị lớn nhất?
![]()
B. 10
![]()
![]()
Chọn A.
Gọi M( x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Biểu diễn hình học của P là đường thẳng và P = 4x + 2y + 3.
Áp dụng bất đẳng thức Bunyakovsky ta có:
P = 4x + 2y + 3 = 4(x – 3) + 2(y – 4) + 23
![]()
Vậy MaxP = 33 
Cho số phức z thỏa mãn z - 3 - 4 i = 1 . Tìm giá trị nhỏ nhất của z .
A. 4
B. 3
C. 5
D. 6
Cho số phức z thỏa mãn z - 3 - 4 i = 1 . Tìm giá trị nhỏ nhất của z .
A. 4
B. 3
C. 5
D. 6
Cho số phức z thỏa mãn |z - 3 - 4i| = 5 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = | z + 2 | 2 - | z - 1 | 2 . Tính mô đun của số phức ω = M + mi
A. | ω | = 1258
B. | ω | = 3 137
C. | ω | = 2 134
D. | ω | = 2 309
Đáp án A
Đặt z = x + yi
Có ![]()
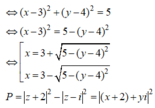
![]()
TH1:
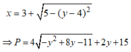
Xét hàm số: ![]() trên
trên ![]()
Có

Ta có:
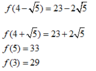
TH2:
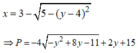
Xét hàm số: ![]() trên
trên ![]()
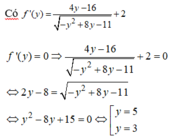
Ta có:
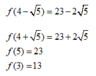
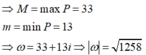
Cho số phức z thỏa mãn z − 3 − 4 i = 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = z + 2 2 − z − i 2 . Tính môđun của số phức w = M + mi
A. w = 2315 .
B. w = 1258 .
C. w = 3 137 .
D. w = 2 309 .
Đáp án B
z = x + y i , ( x , y ∈ ℝ ) ⇒ P = x + 2 2 + y 2 − x 2 - y - 1 2 = 4 x + 2 y + 3 z − 3 − 4 i = 5 ⇔ x - 3 2 + y - 4 2 = 5
Đặt x = 3 + 5 sin t , y = 4 + 5 cost thỏa mãn ( x − 3 ) 2 + ( y − 4 ) 2 = 5
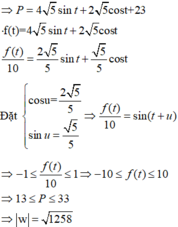
Cho số phức z thỏa mãn z - 3 - 4 i = 5 Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = z - 2 2 - z - i 2 . Tính môđun của số phức w = M + mi
A. w = 2315
B. w = 1258
C. w = 3 137
D. w = 2 309
Đáp án B
z = x + y i , ( x , y ∈ R ) ⇒ P = x + 2 2 + y 2 - x 2 - y - 1 2 = 4 x + 2 y + 3 z - 3 - 4 i = 5 ⇔ x - 3 2 + y - 4 2 = 5
Đặt x = 3 + 5 sin t , y = 4 + 5 cos t thỏa mãn x - 3 2 + y - 4 2 = 5
⇒ P = 4 5 sin t + 2 5 cos t + 23 f t = 4 5 sin t + 2 5 cos t f t 10 = 2 5 5 sin t + 5 5 cos t
Đ ặ t c o s u = 2 5 5 sin u = 5 5 ⇒ f t 10 = sin t + u ⇒ - 1 ≤ f t 10 ≤ 1 ⇒ - 10 ≤ f t ≤ 10 ⇒ 13 ≤ P ≤ 33 ⇒ w = 1258