Cho các số thực a, b thỏa mãn 3 16 < b < a < 1 . Tìm giá trị nhỏ nhất của biểu thức P = log a 16 b - 3 256 + 16 log 2 b a a .
A. 15
B. 16
C. 17
D. 18
câu1:
a) Cho các số thực không âm a, b, c thỏa mãn a + b + c =1. Tìm giá trị lớn nhất và giá trị nhỏ
nhất của biểu thức:
P=\(\frac{ab+bc+ca-abc}{a+2b+c}\)
b) Cho các số thực a, b, c thỏa mãn \(^{a^2+b^2+c^2=1}\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P =ab +bc + ca .
Cho các số thực a, b thỏa mãn: a+b=1 Tìm giá trị nhỏ nhất của biểu thức: P= a³ + b³ + a³ + b³
Cho các số thực a, b thỏa mãn 2 5 < a < b < 1 . Tìm giá trị nhỏ nhất của biểu thức T = 27 log a b 2 b + log b 8 5 a − 2 25 − 3.
A. 11
B. 8
C. 9
D. 6
Xét các số thực a, b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15
Cho các số thực a và b thỏa mãn: ( 2 + a ) ( 1 + b ) = 9 2 Giá trị nhỏ nhất của biểu thức: P = 16 + a 4 + 4 1 + b 4 nằm trong khoảng
A. (8,1;8,3)
B. (4;4,2)
C. (8,3;8,5)
D. (12,4;12,6)
Xét các số thực a; b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của P của biểu thức P = log a b 2 a 2 + 3 log b a b
A. 19.
B. 13.
C. 14.
D. 15.
Chọn D.
Ta có:
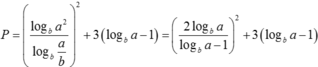
Đặt t = logba – 1 > logbb – 1 = 0; khi đó:
![]()
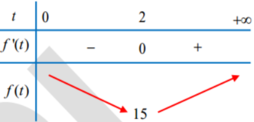
Ta có: ![]()
Và f’(t) = 0 khi 3t3 - 8( t + 1) = 0 hay t = 2.
Suy ra Pmin = f(2) = 15
Xét các số thực a; b thỏa mãn a > b > 1 Tìm giá trị nhỏ nhất Pmin của biểu thức P = log a b 2 a 2 + 3 log b a b
A.19
B.13
C.14
D.15
cho a,b,c là các số thực thỏa mãn a,b≥0;0≤c≤1 và a2+b2+c2 =3.Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=ab+bc+ca+3(a+b+c)
\(P\le a^2+b^2+c^2+3\sqrt{3\left(a^2+b^2+c^2\right)}=12\)
\(P_{max}=12\) khi \(a=b=c=1\)
Lại có: \(\left(a+b+c\right)^2=3+2\left(ab+bc+ca\right)\ge3\Rightarrow a+b+c\ge\sqrt{3}\)
\(a+b+c\le\sqrt{3\left(a^2+b^2+c^2\right)}=3\)
\(\Rightarrow\sqrt{3}\le a+b+c\le3\)
\(P=\dfrac{\left(a+b+c\right)^2-\left(a^2+b^2+c^2\right)}{2}+3\left(a+b+c\right)\)
\(P=\dfrac{1}{2}\left(a+b+c\right)^2+3\left(a+b+c\right)-\dfrac{3}{2}\)
Đặt \(a+b+c=x\Rightarrow\sqrt{3}\le x\le3\)
\(P=\dfrac{1}{2}x^2+3x-\dfrac{3}{2}=\dfrac{1}{2}\left(x-\sqrt{3}\right)\left(x+6+\sqrt{3}\right)+3\sqrt{3}\ge3\sqrt{3}\)
\(P_{min}=3\sqrt{3}\) khi \(x=\sqrt{3}\) hay \(\left(a;b;c\right)=\left(0;0;\sqrt{3}\right)\) và hoán vị
Xét các số thực a, b thỏa mãn a > b > 1. Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b .
A. P min = 19.
B. P min = 13.
C. P min = 14.
D. P min = 15.