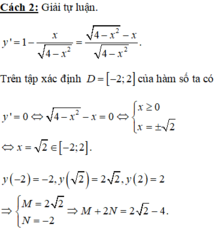Gọi M và N lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức A = cos x + 1 2 sin x + 4 . Giá trị của M+N bằng
A. 3 2
B. 1 3
C. 3 4
D. 2 3
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 . cos x 2 - 3 . sin x + cos x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D . 2 + 3 + 2
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số ![]() trên Biểu thức có giá trị bằng:
trên Biểu thức có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D. 2 + 3 + 2
Đáp án C
Ta có:
![]()
Áp dụng bất đẳng thức Bunhicopxki, có
![]()
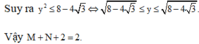
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 cos x 2 - 3 sin x + c o s x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D. 2 + 3 + 2
Đáp án C
Ta có y = - 1 + 2 - 3 . 2 sin x c o s x + 2 cos 2 x = 2 - 3 . sin 2 x + cos 2 x .
Áp dụng bất đẳng thức Bunhicopxki, có
2 - 3 . sin 2 x + cos 2 x 2 ≤ 2 - 3 2 + 1 2 . sin 2 2 x + cos 2 2 x = 8 - 4 3
Suy ra y 2 ≤ 8 - 4 3 ⇔ 8 - 4 3 ≤ y ≤ 8 - 4 3 . Vậy M + N + 2 = 2.
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = − 1 + 2 c o s x 2 − 3 sin x + c o s x trên R. Biểu thức M + N + 2 có giá trị bằng:
A. 0.
B. 4 2 − 3 .
C. 2.
Đáp án C
Ta có: y = − 1 + 2 − 3 .2 sin x cos x + 2 cos 2 x
= 2 − 3 . sin 2 x + cos 2 x
Áp dụng bất đẳng thức Bunhiacopxki, có:
2 − 3 . sin 2 x + cos 2 x 2 ≤ 2 − 3 2 + 1 2 . sin 2 2 x + cos 2 2 x = 8 − 4 3
Suy ra y 2 ≤ 8 − 4 3 ⇔ − 8 − 4 3 ≤ y ≤ 8 − 4 3 .
Vậy M + N + 2 = 2
a) Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P=3\cos2x+2\cos^2x\). Tính T=19M+5m
b) Viết phương trình chính tắc của elip đi qua điểm A(\(\left(2;\sqrt{3}\right)\) và tỉ số của độ dài trục lớn với tiêu cự bằng \(\dfrac{2}{\sqrt{3}}\)
Cho x ; y ∈ R thỏa mãn x + y ≠ - 1 và x 2 + y 2 + x y = x + y + 1 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x y x + y + 1 . Tính M + m
A . 1 3
B . - 2 3
C . 1 2
D . - 1 3
Cho hàm số f ( x ) = x 3 - 3 x . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=|f(sinx+1)+2|. Giá trị biểu thức M + m bằng
A. 4.
B. 6.
C. 2.
D. 8.
Gọi M, N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 4 - x 2 . Giá trị của biểu thức (M + 2N) là
A. 2 2 + 2
B. 4 - 2 2
C. 2 2 - 4
D. 2 2 - 2
Chọn C
Tập xác định của hàm số: D = [-2;2]
Ta có 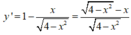
![]()
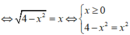
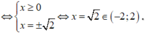
Ta lại có ![]()
Từ đó suy ra ![]()
Vậy ![]()
Gọi M,N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 4 - x 2 Giá trị của biểu thức M + 2 N là
A. 2 2 + 2
B. 4- 2 2
C. 2 2 -4
D. 2 2 -2
Chọn C.
Tập xác định của hàm số ![]()
Cách 1: Bấm máy tính. Với máy 580vn chọn start:-2, end: 2, step: 2/9 có: ![]()
thử thấy phương án C gần nhất với kết quả này nên ta chọn C.