Đáp án C
Ta có:
![]()
Áp dụng bất đẳng thức Bunhicopxki, có
![]()
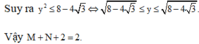
Đáp án C
Ta có:
![]()
Áp dụng bất đẳng thức Bunhicopxki, có
![]()
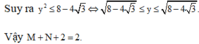
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 . cos x 2 - 3 . sin x + cos x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D . 2 + 3 + 2
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x + cos 2x trên đoạn 0 , π . Khi đó 2M + m bằng
A. 4
B. 5/2
C. 7/2
D. 5
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 . sin 2 x - cos x + 1 . Giá trị M + m bằng:
A. 0
B. 2
C. 25/8
D. 41/8
Gọi M và N lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức A = cos x + 1 2 sin x + 4 . Giá trị của M+N bằng
A. 3 2
B. 1 3
C. 3 4
D. 2 3
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2. sin x trên
đoạn - π 6 , 5 π 6 . Tính M, m.
A. M= 1, m = -1
B. M = 2, m = -2
C. M =1, m = -2
D. M = 2, m = -1
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 + ( k 2 - k + 1 ) x trên đoạn [-1;2]. Khi k thay đổi trên ℝ , giá trị nhỏ nhất của M - m bằng.
![]()
![]()
![]()
![]()
Cho hai số thực x,y thỏa mãn 0 ≤ x ≤ 1 2 , 0 ≤ y ≤ 1 2 , và log ( 11 - 2 x - y ) = 2 y + 4 x - 1 . Xét biểu thức P = 16 y x 2 - 2 x ( 3 y + 2 ) - y + 5 . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của T = ( 4 m + M ) bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Gọi M và m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số f x = sin 4 x + cos 2 x + 1 4 cos 2 x . Giá trị M - m bằng
A. 1 16
B. 9 16
C. 1 2
D. 11 16
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = cos x + 2 . sin x + 3 2 . cos x - sin x + 4 . Tính M,m
A. 4/11
B. 3/4
C. 1/2
D. 20/11