Tìm tất cả các giá trị của tham số m sao cho đồ thị (Cm) của hàm số y = m x + 3 1 - x có tiệm cận và tâm đối xứng của đồ thị thuộc đường thẳng d:2x-y+1=0
A. với mọi m
B. không có m
C. m = 3
D. m = -3
Tìm tất cả các giá trị của tham số m sao cho đồ thị C m của hàm số y = m x + 3 1 - x có tiệm cận và tâm đối xứng của đồ thị thuộc đường thẳng d : 2 x - y + 1 = 0
A. với mọi m
B. không có m
C. m = 3
D. m = -3
Chọn B
Điều kiện để đồ thị có tiệm cận: m ≠ - 3
Tâm đối xứng I(1;-m) là giao điểm của hai đường tiệm cận.
Khi đó, I ∈ d ⇔ m = - 3 (loại). Vậy không tồn tại m thỏa mãn.
Cho hàm số y = x 3 − 3 x 2 + m + 1 x + 1 có đồ thị C m với m là tham số. Tìm tất cả các giá trị của tham số m để đường thẳng d : y = x + 1 cắt đồ thị C m tại ba điểm phân biệt P 0 ; 1 , M , N sao cho tam giác OMN vuông tại O (O là gốc tọa độ)
A. m = -2
B. m = -6
C. m = -3
D. m = -1
Cho hàm số y = x 3 - 3 x 2 + ( m + 1 ) x + 1 có đồ thị ( C m ) với m là tham số. Tìm tất cả các giá trị của tham số m để đường thẳng d : y = x + 1 cắt đồ ( C m ) thị tại ba điểm phân biệt P(0;1) sao cho tam giác OMN vuông tại O (O là gốc tọa độ)
A. m = -2
B. m = -6
C. m = -3
D. m = - 7 2
tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y=\dfrac{\sqrt{1-x}}{x-m}\) có tiệm cận đứng .
ĐKXĐ: \(x\le1\)
Hàm có tiệm cận đứng khi và chỉ khi phương trình:
\(x-m=0\) có nghiệm \(x< 1\)
\(\Leftrightarrow m< 1\)
Cho hàm số y = x 3 - 3 x 2 + ( m + 1 ) x + 1 có đồ thị c m với m là tham số. Tìm tất cả các giá trị của tham số m để đường thẳng d : y = x + 1 cắt đồ thị c m tại ba điểm phân biệt P ( 0 ; 1 ) , M , N sao cho tam giác OMN vuông tại O (O là gốc tọa độ)
A. m = -2
B. m = -6
C. m = -3
D. m = - 7 2
Đáp án A.
Phương trình hoành độ giao điểm của c m và d : x 3 - 3 x 2 + ( m + 1 ) x + 1 = x + 1
⇔ x 3 - 3 x 2 + m x = 0 ⇔ x = 0 x 2 - 3 x + m = 0 *
Để c m cắt d tại ba điểm phân biệt P ( 0 ; 1 ) , M , N thì phương trình (*) phải có hai nghiệm phân biệt x 1 , x 2 khác 0 ⇔ 0 2 - 3 . 0 + m ≢ 0 ∆ = ( - 3 ) 2 - 4 m > 0 ⇔ m ≢ 0 m < 9 4
Giả sử M ( x 1 ; x 1 + 1 ) vàvới N ( x 2 ; x 2 + 1 ) là nghiệm của phương trình (*).
Theo định lý Vi-ét ta có x 1 + x 2 = 3 x 1 x 2 = m
Để tam giác OMN vuông tại O thì O M → . O N → = 0 ⇔ x 1 x 2 + ( x 1 + 1 ) ( x 2 + 1 ) = 0
⇔ 2 x 1 x 2 + ( x 1 + x 2 ) + 1 = 0 ⇔ 2 m + 4 = 0 ⇔ m = - 2 (thỏa mãn)
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y = x 2 - x - m + 1 x - m không có tiệm cận đứng.
A. m = 1
B. m = ± 1
C. m = -1
D. m ≠ 1
Đáp án A.
Đồ thị hàm số không có tiệm cận đứng
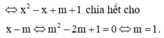
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y = x + 1 m 2 x 2 + m − 1 có bốn đường tiệm cận.
A. m < 1 hoặc m>1
B. với mọi giá trị m
C. m > 0
D. m < 1 và m ≠ 0
Đáp án là D.
Đồ thị hàm số có bốn đường tiệm cận khi phương trình m 2 x 2 + m − 1 = 0 có hai nghiệm phân biệt khác -1 ⇔ m 2 ≠ 0 − m 2 m − 1 > 0 ⇔ m ≠ 0 m < 1 .
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = x + 1 x 3 - 3 x 2 - m có đúng một tiệm cận đứng.
A.Mọi m
B.
C.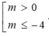
D.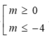
TH1 : Phương trình x3-3x2-m=0 có một nghiệm đơn x= -1 và một nghiệm kép.
Phương trình x3-3x2-m=0 có nghiệm x=-1 nên (-1)3-3(-1)2-m=0 hay m = -4.
Với m= -4 phương trình trở thành 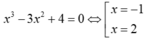
(thỏa mãn vì x=2 là nghiệm kép).
TH2: Phương trình x3-3x2-m=0 có đúng một nghiệm khác -1 hay x3-3x2=m có một nghiệm khác -1
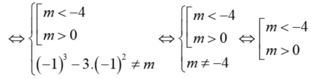
Vậy với 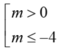 thỏa mãn yêu cầu đề bài.
thỏa mãn yêu cầu đề bài.
Chọn C.
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = x + 1 x 3 - 3 x 2 - m có đúng một tiệm cận đứng.
A. m> 0
B. m < -4
C. m> 0 hoặc m ≤ - 4
D. m< 3
TH1 : Phương trình x3- 3x2-m=0 có một nghiệm đơn x= -1 và một nghiệm kép.
Phương trình x3- 3x2-m=0 có nghiệm x= -1 nên ( -1) 3-3( -1) 2-m=0 hay m= -4.
Với m= -4 phương trình trở thành
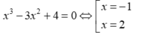
(thỏa mãn vì x= 2 là nghiệm kép).
TH2: Phương trình x3- 3x2-m=0 có đúng một nghiệm khác – 1 hay x3- 3x2= m có một nghiệm khác -1
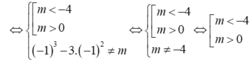
Vậy với m> 0 hoặc m≤ - 4 thỏa mãn yêu cầu đề bài.
Chọn C.