Tìm môđun của số phức z=a+bi (a,bÎR) thỏa mãn z - 4 = 1 + i z - 4 + 3 z i
A. z = 1
B. z = 1 2
C. z = 2
D. z = 4
Tìm môđun của số phức z=a+bi a , b ∈ R thỏa mãn ( z - 4 ) = ( 1 - i ) z - ( 4 + 3 z ) i
![]()
![]()
![]()
![]()
Xét các số phức z = a + b i (a,bÎR) thỏa mãn z - 4 - 3 i = 5 . Tính a+b khi z + 1 - 3 i + z - 1 + i đạt giá trị lớn nhất
A. 10
B. 4
C. 6
D. 8
Tìm môđun của số phức\(z=a+bi\) \(\left(a,b\in R\right)\) thỏa mãn \(z-4=\left(1+i\right)\left|z\right|-\left(4+3z\right)i\)
\(\Leftrightarrow z\left(3i+1\right)=\left(\left|z\right|-4\right)i+\left|z\right|+4\)
Lấy module 2 vế:
\(\Rightarrow\left|z\right|.\sqrt{10}=\sqrt{\left(\left|z\right|-4\right)^2+\left(\left|z\right|+4\right)^2}\)
Đặt \(\left|z\right|=x>0\Rightarrow x\sqrt{10}=\sqrt{\left(x-4\right)^2+\left(x+4\right)^2}\)
\(\Leftrightarrow10x^2=2x^2+32\)
\(\Leftrightarrow x^2=4\)
\(\Rightarrow x=2\)
Vậy \(\left|z\right|=2\)
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z = a + b i (a,bÎR) thỏa mãn z + 2 + i - z 1 + i và z 2 > 1 . Tính giá trị của biểu thức P = a + b
A. -1
B. -5
C. 3
D. 7
Cho số phức z thỏa mãn ![]() z
(
1
-
2
i
)
+
z
¯
i
=
15
+
i
z
(
1
-
2
i
)
+
z
¯
i
=
15
+
i
Tìm môđun của số phức z.
A. z = 5
B. z = 4
C. z = 2 5
D. z = 2 3
Đáp án A
Phương pháp
Gọi ![]()
Sử dụng định nghĩa hai số phức bằng nhau.
Cách giải
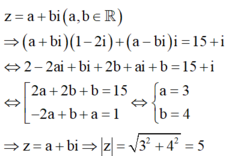
Cho số phức z thỏa mãn z - 1 + 2 i =3 . Tìm môđun nhỏ nhất của số phức z-1 +i
A. 4
B. 2 2
C. 2
D. 2
Cho số phức z thỏa mãn z = ( 1 - 3 i ) 3 1 - i . Tìm môđun của z - i . z
A. 8 2
B. 8
C. 4 2
D. 4.
Cho số phức z thỏa mãn ( 1 - i ) z - 6 - 2 i = 10 . Tìm môđun lớn nhất của số phức z
A. 4 5
B. 3 5
C. 3
D. 3 + 5