Trong mặt phẳng tọa độ Oxy, gọi (H) là tập hợp điểm biểu diễn số phức w = ( 1 + 3 i ) z + 2 thỏa mãn | z - 1 | ≤ 2 . Tính diện tích của hình (H).
A. 8 π .
B. 12 π .
C. 16 π .
D. 4 π .
Trong mặt phẳng tọa độ Oxy, cho số phức z thỏa mãn z - 1 + 2 i = 3 . Tập hợp các điểm biểu diễn cho số phức w=z(1+i) là đường tròn
A. Tâm I(3;-1); R = 3 2
B. Tâm I(3;-1);R=3
C. Tâm I(-3;1); R = 3 2
D. Tâm I(3;-1);R=3
Xét các số phức z thỏa mãn điều kiện z - 1 + i = 2 Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức w = z + 2 -i là
A. đường tròn tâm I(-3;2), bán kính R = 2.
B. đường tròn tâm I(3;-2), bán kính R = 2.
C. đường tròn tâm I(1;0), bán kính R =2.
D. đường tròn tâm I(1;-1), bán kính R = 2.
Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy để ![]() số phức z có phần thực không âm. Tính diện tích hình (H).
số phức z có phần thực không âm. Tính diện tích hình (H).
![]()
![]()
Chọn A.
+ Giả sử z = a + bi, khi đó ![]() , giả thiết của bài toán là
, giả thiết của bài toán là
![]()
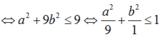
+ Vậy tập hợp các điểm biểu diễn cho số phức z là điểm M(a; b) thuộc miền trong của elip 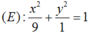 (kể cả các điểm trên biên).
(kể cả các điểm trên biên).
+ Bán trục lớn của ( E) là a = 3, bán trục bé của ( E) là b = 1 nên diện tích cần tính của miền ( H) là S = πab = 3π.
Gọi H là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy sao cho 2 z - z ≤ 3 và số phức z có phần ảo không âm. Tính diện tích hình H
A. 3π
B. 3 π 4
C. 3 π 2
D. 6π
Gọi H là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy sao cho 2 z - z ¯ ≤ 3 và số phức z có phần ảo không âm. Tính diện tích hình H
A. 3 π
B. 3 π 4
C. 3 π 2
D. 6 π
Chọn C.
Phương pháp: Xác định hình H từ đó tính diện tích.


Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn 1 < z < 3
A. Phần hình phẳng nằm hoàn toàn phía ngoài hình tròn (O,1) và phía trong hình tròn (O,3)
B. Hình tròn (O,3) (bỏ gốc tọa độ O)
C. Hình tròn (O,1) (bỏ gốc tọa độ O)
D. Đường tròn (O,1)
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn 1 < z < 3

![]()
![]()
![]()
Cho z 1 , z 2 là hai số phức thỏa mãn điều kiện z - 5 - 3 i = 5 đồng thời z 1 - z 2 = 8 . Tập hợp các điểm biểu diễn số phức w = z 1 + z 2 trong mặt phẳng tọa độ Oxy là đường tròn có phương trình
A. x - 10 2 + y - 6 2 = 36
B. x - 10 2 + y - 6 2 = 16
C. x - 5 2 2 + y - 3 2 2 = 9
D. x - 5 2 2 + y - 3 2 2 = 9 4
Cho z 1 , z 2 là hai số phức thỏa mãn điều kiện |z-5-3i|=5 đồng thời z 1 - z 2 = 8 . Tập hợp các điểm biểu diễn số phức w = z 1 + z 2 trong mặt phẳng tọa độ Oxy là đường tròn có phương trình
A. x - 10 2 + y - 6 2 = 36
B. x - 10 2 + y - 6 2 = 16
C. x - 5 2 2 + y - 3 2 2 = 9
D. x - 5 2 2 + y - 3 2 2 = 9 4
Tập hợp điểm biểu diễn số phức z=x+yi thỏa mãn |z-5-3i|=5 là đường tròn tâm I(5;3) bán kính R=5
Gọi M 1 ( x 1 ; y 1 ) ; M 2 ( x 2 ; y 2 ) là hai điểm biểu diễn các số phức z 1 ; z 2 thì từ z 1 - z 2 = 8 ta suy ra M 1 M 2 = 8
Gọi N(x;y) là điểm biểu diễn số phức w = z 1 + z 2 thì x = x 1 + x 2 y = y 1 + y 2
Gọi M là trung điểm M 1 M 2 thì M x 1 + x 2 2 ; y 1 + y 2 2
Ta có:
![]()
hay 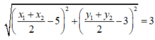
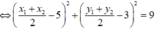
![]()
![]()
Vậy tập hợp các điểm N thỏa mãn bài toán là đường tròn
![]() .
.
Chọn đáp án A.