Gọi A là tập hợp tất cả các số tự nhiên có 8 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc A. Tính xác suất để số tự nhiên được chọn chia hết cho 25.
A. 17 81 .
B. 43 324 .
C. 1 27 .
D. 11 324 .
Gọi A là tập hợp tất cả các số tự nhiên có 8 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc A. Tính xác suất để số tự nhiên được chọn chia hết cho 25
A. 17 81
B . 43 324
C. 1 27
D. 11 324
Gọi A là tập hợp tất cả các số tự nhiên có tám chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc A. Tính xác suất để số tự nhiên được chọn chia hết cho 45
A. 2 81
B. 53 2268
C. 1 36
D. 5 162
Gọi A là tâp hợp các số tự nhiên có 8 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc vào tập A. Tính xác suất để chọn được số chia hết cho 9.
Số các số có `8` chữ số đôi một khác nhau là `9.A_9^7`(số)
`=> n(A) = n(\Omega) = 9.A_9^7`
Dễ thấy rằng `0 + 1 + 2 + .. + 9 = 45 \vdots 9`
Gọi `X = {0;1;..;9}`
Để số đó chia hết cho `8` thì nó phải được chọn từ các tập
`X \\ {0;9}` , `X \\ {1;8}` , `X \\ {2;7}` , `X \\ {3;6}` , `X \\ {4;5}`
Ta xét `2` trường hợp như sau:
Trường hợp `1`: Số đó được chọn từ tập `X \\ {0;9}`
Xếp `8` số vào `8` vị trí có `8!`(cách)
Trường hợp `2`:Số đó được chọn từ `4` tập còn lại
Chọn `1` trong `4` tập có `C_4^1`(cách)
Xếp `8` chữ số vừa chọn `1` cách ngẫu nhiên có `8!`(cách)
Cho số `0` đứng đầu xếp `7` số còn lại có `7!` cách
Số lập được:`4(8!-7!)`(số)
Gọi `B` là biến cố chọn được số chia hết cho `9` từ tập `A`
`=> |B| = 8! + 4(8!-7!)`
Xác xuất biến cố `B`:
`P(B) = \frac{8!+4(8!-7!)}{9.A_9^7} = \frac{1}{9}`
Gọi A là tập hợp các số tự nhiên có 5 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số tự nhiên thuộc tập A. Tính xác suất để chọn được một số thuộc A và số đó chia hết cho 5.
A. P = 11 27
B. P = 53 243
C. P = 2 9
D. P = 17 81
HD: Có 9.9.8.7.6 = 27216 số có 5 chữ số đôi một khác nhau

Gọi S là tập hợp tất cả các số tự nhiên gồm 3 chữ số. Chọn ngẫu nhiên một số thuộc S. Xác suất để số chọn được là một số tự nhiên chia hết cho 9 và có các chữ số đôi một khác nhau bằng
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các số tự nhiên gồm 3 chữ số. Chọn ngẫu nhiên một số thuộc S. Xác suất để số chọn được là một số tự nhiên chia hết cho 9 và có các chữ số đôi một khác nhau bằng
A . 19 225
B . 29 450
C . 16 225
D . 7 75
Chọn A
+) Không gian mẫu Ω = “Chọn ngẫu nhiên một số trong các số tự nhiên có 3 chữ số”.=> | Ω | = 9. 10 2
+) Biến cố A = “Số tự nhiên được chọn chia hết cho 9 và các chữ số đôi một khác nhau”.
Ta tìm số các số tự nhiên gồm 3 chữ số khác nhau và chia hết cho 9 (tổng các chữ số là một số chia hết cho 9).
Bộ ba số (a;b;c) với a,b,c ∈ [0;9](a,b,c đôi một khác nhau ) và a + b + c = 9m, m ∈ ℕ * được liệt kê dưới đây:

Vậy có tất cả 10.3! + 4.2.2! = 76 => | Ω A | = 76
Xác suất cần tính bằng 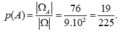
Gọi S là tập hợp tất cả các số tự nhiên có 3 chữ số đôi một khác nhau được lập từ các chữ số 0,1,2,3,4,5,6. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số chia hết cho 6
Gọi A là tập hợp tất cả các số tự nhiên gồm bốn chữ số đôi một khác nhau được chọn từ các chữ số 1; 2; 3; 4; 5; 6. Chọn ngẫu nhiên một số từ tập A. Xác suất để số chọn được là số chia hết cho 5 là
A. 2/3
B. 1/6
C. 1/30
D. 5/6
Gọi A là tập hợp tất cả các số tự nhiên gồm bốn chữ số đôi một khác nhau được chọn từ các chữ số 1 ; 2 ; 3 ; 4 ; 5 ; 6 . Chọn ngẫu nhiên một số từ tập A . Xác suất để số chọn được là số chia hết cho 5 là
A. 2 3 .
B. 1 6 .
C. 1 30 .
D. 5 6 .