Trong không gian Oxyz, cho tam giác OAB với O(0;0;0), A(-1;8;1), B(7;-8;5) . Phương trình đường cao OH của tam giác OAB là
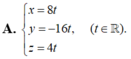
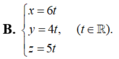
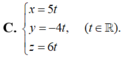

Trong không gian Oxyz, cho tam giác OAB với O ( 0 ; 0 ; 0 ) , A ( − 1 ; 8 ; 1 ) , B ( 7 ; − 8 ; 5 ) . Phương trình đường cao OH của tam giác OAB là
A. x = 8 t y = − 16 t , z = 4 t ( t ∈ ℝ ) .
B. x = 6 t y = 4 t , z = 5 t ( t ∈ ℝ ) .
C. x = 5 t y = − 4 t , z = 6 t ( t ∈ ℝ ) .
D. x = 5 t y = 4 t , z = 6 t ( t ∈ ℝ ) .
Đáp án D
Để ý rằng OH nằm trong mặt phẳng (OAB) và OH vuông góc với AB, nên một vecto chỉ phương của OH là tích có hướng của A B → và vecto pháp tuyến của mặt phẳng (OAB).
Trong không gian với hệ tọa độ Oxyz ,cho tam giác OAB có A − 1 ; − 1 ; 0 , B 1 ; 0 ; 0 . Tính độ dài đường cao kẻ từ O của tam giác OAB
A. 1 5
B. 5
C. 5 10
D. 2 5 5
Đáp án A
Ta có: A B → 2 ; 1 ; 0 , O B → 1 ; 0 ; 0 ⇒ d O , A B = A B → ; O B → A B → = 1 5
Trong không gian với hệ tọa độ Oxyz ,cho tam giác OAB có A(-1;-1;0), B(1;0;0) . Tính độ dài đường cao kẻ từ O của tam giác OAB
A. 1 5
B. 5
C. 5 10
D. 2 5 5
Trong không gian với hệ tọa độ Oxyz, cho tam giác OAB có A ( - 1 ; - 1 ; 0 ) , B ( 1 ; 0 ; 0 ) . Tính độ dài đường cao kẻ từ O của tam giác OAB.
A. 1 5
B. 5
C. 5 10
D. 2 5 5
Đáp án A
Phương pháp:
Công thức khoảng cách từ điểm đến đường thẳng trong không gian:
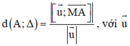 là VTCP của Δ và M là điểm bất kì thuộc
là VTCP của Δ và M là điểm bất kì thuộc
Cách giải:

Độ dài đường cao kẻ từ O của tam giác OAB bằng khoảng cách từ O đến đường thẳng AB:
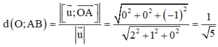
Trong không gian Oxyz, cho hai điểm A 2 ; 2 ; 1 , B - 8 3 ; 4 3 ; 8 3 . Đường phân giác trong góc O của tam giác OAB có phương trình là
A. x = 0 y = t z = t
B. x = 4 t y = t z = - t
C. x = 14 t y = 2 t z = - 5 t
D. x = 2 t y = 14 t z = 13 t
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S = x 2 + y 2 + z 2 - 4 x - 4 y - 4 z = 0 và điểm ( 4;4;0 ).
Viết phương trình mặt phẳng ( OAB ),
biết điểm B ∈ S và tam giác OAB đều.
A. x - y + z = 0; x + y - z = 0
B. x - y + z = 0; x - y - z = 0
C. x - y - z = 0; x - y - z = 0
D. x - y + z = 0; x - y + z = 0
(S) có tâm I ( 2;2;2 ), bán kính R = 2 3 . Nhận thấy O và A đều thuộc (S). Tam giác OAB đều, có bán kính đường tròn ngoại tiếp r = O A 3 = 4 2 3
Khoảng cách d ( I; (P) ) = R 2 - r 2 = 2 3
(P) đi qua O có phương trình dạng: ax + by +cz = 0
(P) đi qua A, suy ra b = -a
d ( I; (P) ) = 2 3 ⇔ 2 a + b + c a 2 + b 2 + c 2 = 2 3
⇔ 2 c 2 a 2 + c 2 = 2 3 ⇔ 4 c 2 2 a 2 + c 2 = 4 3 ⇔ 12 c 2 = 8 a 2 + 4 c 2 ⇔ c 2 = a 2 ⇔ c = ± a
Vậy có hai mặt phẳng cần tìm: x - y + z = 0; x - y - z = 0
Đáp án B
Trong không gian Oxyz, cho tam giác OAB với O(0;0;0),A(6;0;0),B(0;8;0). Điểm M(a;b;c)thuộc mặt phẳng (P): x+2y+3z-2=0 đồng thời cách đều các đỉnh O, A, B. Giá trị của tổng a+b-c là
A. -2.
B. 2.
C. 4.
D. 10
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 2 x - 2 y - 2 z = 0 và điểm A 2 ; 2 ; 0 . Viết phương trình mặt phẳng O A B , biết rằng điểm B thuộc mặt cầu S , có hoành độ dương và tam giác OAB đều.
A. x - y + 2 z = 0
B. x - y - 2 z = 0
C. x - y - z = 0
D. x - y + z = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 − 2 x − 2 y − 2 z = 0 và điểm A 2 ; 2 ; 0 . Viết phương trình mặt phẳng O A B , biết rằng điểm B thuộc mặt cầu (S), có hoành độ dương và tam giác OAB đều.
A. x − y − 2 z = 0
B. x − y + z = 0
C. x − y − z = 0
D. x − y + 2 z = 0
Đáp án C.
Đặt B x ; y ; z . Ta có O A 2 = 8, Δ O A B đều ⇒ O A 2 = O B 2 = A B 2 = 8 .
Mà B ∈ S ⇒ Ta có hệ x 2 + y 2 + z 2 − 2 x − 2 y − 2 z = 0 1 x 2 + y 2 + z 2 = 8 (2) x − 2 2 + y − 2 2 + z 2 = 8 (3)
Thế (2) vào (1) và (3) ta được: x + y + z = 4 x + y = 2 ⇔ z = 2 y = 2 − x .
Thế vào (2):
x 2 + 2 − x 2 = 8 ⇔ 2 x 2 − 4 x = 0 ⇔ x = 0 l x = 2
Với x = 2 ⇒ y = 0 ⇒ B 2 ; 0 ; 2
⇒ n → = O A → , O B → = 4 ; − 4 ; − 4 ⇒ Phương trình O A B : x − y − z = 0 .