Tính bán kính mặt cầu ngoại tiếp khối chóp tứ giác đều có cạnh đáy bằng 1 và góc giữa cạnh bên và mặt đáy bằng 60 ° .
A. 6 4
B. 6 2
C. 6 3
D. 6 6
Tính bán kính mặt cầu ngoại tiếp khối chóp tứ giác đều có cạnh đáy bằng 1 và góc giữa cạnh bên và mặt đáy bằng 60 o
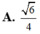

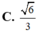
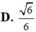
cho hình chóp đều SABC, đáy ABC có cạnh bằng a góc giữa cạnh bên và mặt đáy bằng 60 độ
a, xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp SABC
b, Tính thể tính khối nón ngoại tiếp hình chóp SABC
c, Tính diện tích toàn phần hình trụ có diện tích là tâm đáy trên và tám giác abC là tam giác ngoại tiếp đáy dưới
Cho hình chóp tam giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60 ° . Tính diện tích S của mặt cầu ngoại tiếp hình chóp đã cho.
A. S = 16 πa 2 9
B. S = 64 πa 2 9
C. S = 16 πa 2 3
D. S = 64 πa 2 3
Bán kính mặt cầu ngoại tiếp hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên cùng bằng a là
![]()
![]()
![]()
![]()
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
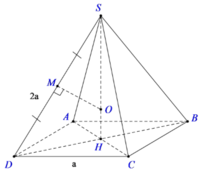
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông ABCD.
Gọi M là trung điểm của SD, trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O. Suy ra; OS = OD (1)
Mà O thuộc trục SH của hình vuông ABCD nên:
OA = OB = OC = OD (2)
Từ (1) và (2) suy ra: OA = OB = OC = OD = OS
Do đó, O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD. Bán kính mặt cầu là R = SO
Ta có:
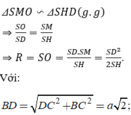
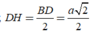
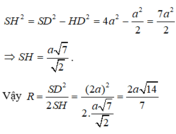
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
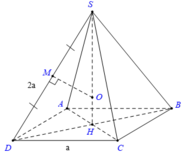
A. 2 a 14 7
B. 2 a 7 2
C. 2 a 7 3 2
D. 2 a 2 7
Đáp án A
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông.
Gọi M là trung điểm của ABCD .
Trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O
Thì OS = OA = OC = OD
Nên O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD .
Bán kính mặt cầu là R = SO.
Ta có:
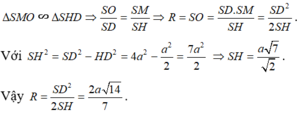
II. Tự luận ( 4 điểm)
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông ABCD.
Gọi M là trung điểm của SD, trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O. Suy ra; OS = OD (1)
Mà O thuộc trục SH của hình vuông ABCD nên:
OA = OB = OC = OD (2)
Từ (1) và (2) suy ra: OA = OB = OC= OD = OS
Do đó, O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD. Bán kính mặt cầu là R = SO
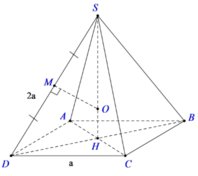
Ta có:

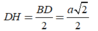
![]()
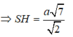
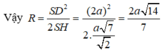
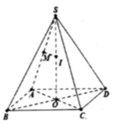
Cho hình chóp tứ giác đều S.ABCD có đáy hợp với cạnh bên một góc 45 o . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD bằng 2 Thể tích khối chóp là?
A. 3 3
B. 4 3 3
C. 3 2 4
D. 4 2 3
Đáp án: D
Hướng dẫn giải:
Gọi O là giao điểm của AC và BD, M là trung điểm của SA.
Qua M kẻ đường thẳng vuông góc với SA cắt SO tại I
⇒ I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD
⇒ S I = R = 2
Ta có:
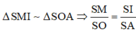
⇒ S O = S M . S A S I = S A 2 2 2
![]()
⇒ S A = S O 2
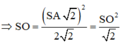
![]()
⇒ A B = 2 ⇒ S A B C D = A B 2 = 4
⇒ V S . A B C D = 1 3 . S O . S A B C D = 4 2 3
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc tạo bởi cạnh bên với đáy bằng 60 ° . Bán kính R mặt cầu ngoại tiếp hình chóp S.ABC là
A. R = a 2
B. R = 2 a 3
C. R = a 3 3
D. R = 4 a 3