Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m - cos x sin 2 x nghịch biến trên ( π 3 ; π 2 ) .
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y= (m-3)x- (2m+1).cos x luôn nghịch biến trên R?
A. - 4 ≤ m ≤ 2 3
B. m> 2
C. m > 3 m ≠ 1
D. m<2
Chọn A.
Tập xác định:D= R. Ta có:y ‘= m-3 + (2m+1).sinx
Hàm số nghịch biến trên R
![]()
Trường hợp 1: m= -1/ 2 ; ta có 0 ≤ 7 2 ∀ x ∈ ℝ
Vậy hàm số luôn nghịch biến trên R.
Trường hợp 2: m< -1/ 2 ; ta có
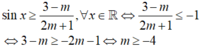
Trường hợp 3:m > -1/2 ; ta có:
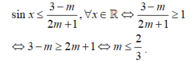
Vậy - 4 ≤ m ≤ 2 3
Tìm tất cả các giá trị của tham số m sao cho hàm số y = cos x + mx đồng biến trên R
A. m > 1
B. m < 1
C. m ≥ 1
D. m ≤ 1
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = - 2 sin x - 1 sin x - m
![]()
![]()
![]()
![]()
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = m cos x + 1 cos x + m đồng biến trên khoảng 0 ; π 3
A. - 1 ; 1
B. - ∞ ; - 1 ∪ 1 ; + ∞
C. [ - 1 ; - 1 2 )
D. - 1 ; - 1 2
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x 4 + 2 m x 2 + m 2 + m có đúng một cực trị.
A. m < 0
B. m > 0
C. m ≥ 0
D. m ≤ 0
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 4 x + m giảm trên khoảng ( - ∞ ; 1 ) ?
A. -2<m<2
B. - 2 ≤ m ≤ - 1
C. - 2 < m ≤ - 1
D. - 2 ≤ m ≤ 2
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 4 x + m giảm trên khoảng - ∞ ; 1
A. - 2 ≤ m ≤ 2
B. - 2 < m < 2
C. - 2 ≤ m ≤ - 1
D. - 2 < m ≤ - 1
Chọn đáp án D
![]() .
.
Ta có y ' = m 2 - 4 x + m 2 .
Hàm số luôn đơn điệu trên từng khoảng - ∞ ; - m và - m ; + ∞ .
Hàm số giảm trên khoảng - ∞ ; 1 tức là hàm số nghịch biến trên khoảng - ∞ ; 1 .
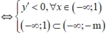
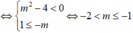
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m - cos x sin 2 x nghịch biến trên π 3 ; π 2
A. m ≤ 5 4
B. m ≥ 1
C. m ≤ 2
D. m ≤ 0
Ta có y = m - cos x sin 2 x = m - cos x 1 - cos 2 x
Đặt t = cos x , t ∈ 0 ; 1 2
Xét hàm số g t = m - t 1 - t 2 , t ∈ 0 ; 1 2
Hàm số nghịch biến trên π 3 ; π 2 khi và chỉ khi
g ' t ≤ 0 , ∀ t ∈ 0 ; 1 2 ⇔ m ≤ t 2 + 1 2 t , ∀ t ∈ 0 ; 1 2
Lại xét hàm số h t = t 2 + 1 2 t , ∀ t ∈ 0 ; 1 2
Ta có h ' t = t 2 - 1 2 t 2 > 0 , ∀ t ∈ 0 ; 1 2
Lập bảng biến thiên trên 0 ; 1 2 , ta suy ra m ≤ 5 4 thỏa yêu cầu bài toán.
Đáp án A
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 4 x + m giảm trên khoảng (-∞;1)?
A. -2≤ m ≤ 2
B. -2< m < 2
C. -2≤ m ≤ -1
D. -2< m ≤ -1