Cho tam giác ABC có trung tuyến AM .Tỉ số diện tích giữa tam giác ABM và tam giác ACM là
Cho tam giác ABC AB =6cm AC=10cm tính AC rồi suy ra diện tích tam giác ABC Kẻ AM là đường trung tuyến của tam giác ABC chứng minh diện tích tam giác ABM = diện tích tam giác ACM giúp mình nhanh ạ mai có rồi
a: Sửa đề: BC=10cm và ΔABC vuông tại A
\(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=3\cdot8=24\left(cm^2\right)\)
b: Kẻ AH vuông góc BC
\(S_{ABM}=\dfrac{1}{2}\cdot AH\cdot BM\)
\(S_{ACM}=\dfrac{1}{2}\cdot AH\cdot CM\)
mà BM=CM
nên \(S_{ABM}=S_{ACM}\)
Cho tam giác ABC có AM là trung tuyến(M C BC)
Chứng minh: Diện tích tam giác ABM bằng diện tích tam giác ACM
Từ A kẻ đường thẳng AH vuông góc với BC ( H thuộc BC )
Ta có : \(S_{ABM}=\frac{1}{2}\cdot BM\cdot AH\)(1)
và \(S_{ACM}=\frac{1}{2}\cdot MC\cdot AH\)(2)
Mặt khác ta có AM là đường trung tuyến
=> \(BM=MC\)(3)
Từ (1), (2) và (3) ta có : \(S_{ABM}=S_{ACM}\left(đpcm\right)\)
/ Cho tam giác ABC cân tại A có đường trung tuyến AM . Chứng minh tam giác ABM = tam giác ACM
xét tam giác ABM và tam giác ACM ta có
AM=AM ( cạnh chung)
AB=AC( tam giác ABC cân tại A)
goc MAB = góc MAC ( AM là tia p.g góc BAC)
->tam giac ABM= tam giac ACM (c-g-c)
Xét ΔABM và ΔACM có
BM = CM (GT)
AB = AC (GT)
AM: cạnh chung
⇒ ΔABM = ΔACM (c - c - c)
Cho tam giác đều ABC có cạnh bằng 6cm. Một điểm M nằm trên cạnh BC sao cho BM = 2cm.
a, Tính độ dài của đoạn thẳng AM và tính côsin của góc BAM ;
b, Tính bán kính đường tròn ngoại tiếp tam giác ABM;
c, Tính độ dài đường trung tuyến vẽ từ đỉnh C của tam giác ACM;
d, Tính diện tích tam giác ABM.
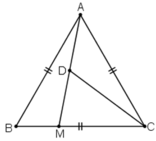
a) Do tam giác ABC là tam giác đều nên 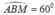 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
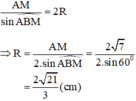
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
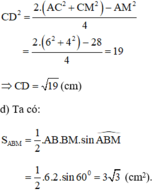
Cho tam giác ABC, lấy M làm điểm chính giữa BC.
a, So sánh diện tích tam giác ABM và diện tích tam giác ACM
b, So sánh diện tích tam giác ABM và diện tích tam giác ABC
Đáp án:
a) Vì M là trung điểm của BC nên BM bằng CM.
Vì hình tam giác ABM và hình tam giác ACM có chung cạnh AM nên độ dài chiều cao của hình tam giác ABM và ABM bằng nhau.
→→Do có chung độ dài đáy và chiều cao bằng nhau nên diện tích hai hình tam giác bằng nhau.
Vậy diện tích hình tam giác ABM bằng diện tích hình tam giác ACM.
b) Vì BM bằng MC nên BM và MC bằng 1212 BC. Do đó diện tích hình tam giác ABM bằng 1/2 diện tích hình tam giác ABC.
Vậy diện tích hình tam giác ABM bằng 1/2 diện tích hình tam giác ABC.
Ht và tk
Cho tam giác ABC vuông tại A,trung tuyến AM,cho biết tam giác ABM là tam giác đều có độ dài cạnh \(\sqrt{3}\)
a.Tính độ dài AC và đyường cao AH của tam giác ABC
b.Tính diện tích tam giác ABC
Cho tam giác ABC,M là trung điểm BC
Chứng minh :a,Diện tích tam giác ABM=diện tích tam giác ACM
b, diện tích ABM =diện tích tam giác ABC/2
Cho tam giác ABC có đường trung tuyến AM. Vẽ hai đường caocủa tam giác BH và CK lần lượt là đường cao của tam giác ABM và ACM. Chứng minh rằng BH = CK.
cho tam giác ABC cân tại A (A nhỏ hơn 90 độ có AM là đường trung tuyến)
a) chứng minh tam giác ABM = tam giác ACM và AM là tia phân giác góc A
b) từ M vẽ ME vuông góc với AB tại E; MF vuông góc với AC tại F, chứng minh tam giác MAE = tam giác MAF và tam giác MEF cân
c) trên tia đối của tia MA lấy điểm H sao cho MA=MH, gọi M là trung điểm (H,y là giao điểm của CB và AN) chứng minh BC bằng 6 lần MI
cần gấp ạ!!