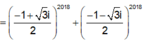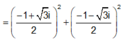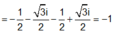Gọi z 1 , z 2 là hai nghiệm của phương trình 3 z 2 - z + 4 = 0 . Khi đó P= z 1 z 2 + z 2 z 1 bằng
A. - 23 12
B. 23 12
C. - 23 24
D. 23 24
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 - z + 2. Tính z 1 2 + z 2 2
A. - 11 9
B. 8 3
C. 2 3
D. 4 3
Gọi z 1 , z 2 là hai nghiệm của phương trình z 2 + z + 1 = 0 Tính P = z 1 2020 + z 2 2020
A. P=1
B. P= -1
C. P=0
D. P=2
Gọi z 1 , z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 2 = 0 . Tính z 1 2 + z 2 2
A. 8/3
B. 2/3
C. 4/3
D. -11/9
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 − z + 2 = 0. Tính z 1 2 + z 2 2
A. − 11 9
B. 8 3
C. 2 3
D. 4 3
Đáp án D
z 2 − z + 2 = 0 ⇔ z = 1 ± i 23 6 ⇒ z 1 = z 2 = 2 3
Khi đó z 1 2 + z 2 2 = 4 3
Gọi z 1 , z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 2 = 0 Tính z 1 2 + z 2 2
A. - 11 9
B. 8 3
C. 2 3
D. 4 3
Gọi z 1 , z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 2 = 0 . Tính | z 1 | 2 + | z 2 | 2
A. -11/9
B. 8/3
C. 2/3
D. 4/3
Gọi z 1 ; z 2 là hai nghiệm phức của phương trình z 2 + z + 1 = 0 . Giá trị của P = z 1 2019 + z 2 2019 là
A. P = 2
B. P = 3
C. P = 2 3
D. P = 4038
Trong tập các số phức gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 với z 2 có phần ảo dương. Cho số phức z thỏa mãn |z- z 1 | = 1 Giá trị nhỏ nhất của P = |z- z 2 | là
A . 2016 - 1
B . 2017 - 1
C . 2017 - 1 2
D . 2016 - 1 2
Đáp án A
Phương trình 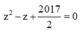
![]()
![]()
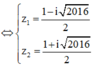
Ta có ![]()
![]()
![]()
Vật giá trị nhỏ nhất của biểu thức P là ![]()
Gọi z 1 và z 2 là hai nghiệm phức của phương trình z 2 + z + 1 = 0 . Tính giá trị của z 1 2017 + z 2 2017
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án C
Phương pháp: Tính z 1 , z 2 và sử dụng công thức Moivre
Cách giải: Phương trình z 2 + z + 1 có ∆ = 1 - 4 = - 3 nên có 2 nghiệm
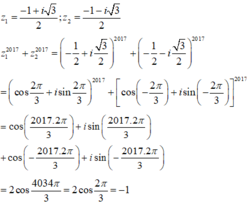
Gọi z1, z2 là hai nghiệm của phương trình z 2 + z + 1 = 0. Tính giá trị của biểu thức z 1 2018 + z 2 2018 ?
A. 2 2019
B. 2 1010
C. 1.
D. -1
Đáp án D
Cách 1: Em có z = 1 không là nghiệm của phương trình trên.
![]()
![]()
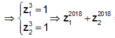
![]()
![]()
Theo định lý Vi-ét em có
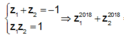
![]()
Cách 2: Em có
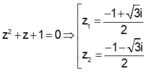
![]()