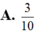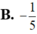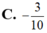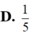Đáp án A
Phương trình 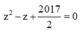
![]()
![]()
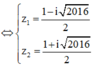
Ta có ![]()
![]()
![]()
Vật giá trị nhỏ nhất của biểu thức P là ![]()
Đáp án A
Phương trình 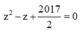
![]()
![]()
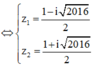
Ta có ![]()
![]()
![]()
Vật giá trị nhỏ nhất của biểu thức P là ![]()
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 . Giá trị nhỏ nhất của P = z - z 2 là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 Giá trị nhỏ nhất của P = z - z 2 là
![]()
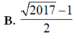
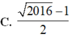
![]()
Trong tập hợp các số phức, gọi z 1 ; z 2 là nghiệm của phương trình z 2 - z + 2017 4 = 0 , với z 2 có thành phần ảo dương. Cho số phức z thoả mãn z - z 1 = 1 . Giá trị nhỏ nhất của P = z - z 2 là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1
Biết rằng hai số phức z 1 , z 2 thỏa mãn | z 1 - 3 - 4 i | = 1 và | z 2 - 3 - 4 i | = 1 2 . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3 a - 2 b = 12 . Giá trị nhỏ nhất của P = | z - z 1 | + | z - 2 z 2 | + 2 bằng:
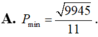
![]()
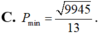
![]()
Cho số phức z thỏa mãn z - 1 + 3 i + z ¯ + 5 + i = 2 65 Giá trị nhỏ nhất của z + 2 + i đạt được khi z = a + b i với a,b là các số thực dương. Giá trị của 2 a 2 + b 2 bằng
![]()
![]()
![]()
![]()
Trong các số phức z thỏa mãn điều kiện z + 2 - 3 i = z + 1 - 2 i , hãy tìm phần ảo của số phức có môđun nhỏ nhất?
A. 10 13
B. 2 5
C. -2
D. - 2 13
Trong các số phức z thỏa mãn z - 1 + i = z + 1 - 2 i , số phức z có mô đun nhỏ nhất có phần ảo là
A. 3 10
B. 3 5
C. - 3 5
D. - 3 10
Cho z là các số phức thỏa mãn điều kiện z + 3 1 - 2 i + 2 = 1 và w là số thuần ảo.
Giá trị nhỏ nhất của biểu thức z - w bằng
A. 5 - 5
B. 5
C. 2 2
D. 1 + 3
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn z + 1 + i = z ¯ + i . Tổng phần thực và phần ảo của số phức z bằng