Có bao nhiêu số phức z = a + b i a , b ∈ R thỏa mãn z + i + z - 3 i = z + 4 i + z - 6 i và z ≤ 10
A. 12
B. 5
C. 2
D. 10
Gọi T là tập hợp các số phức z thỏa mãn z - i ≥ 3 và z - 1 ≤ 5 . Gọi z 1 , z 2 ∈ T lần lượt là các số phức có môdun nhỏ nhất và lớn nhất. Tìm số phức z 1 + 2 z 2
A. 12+2i
B. -2+12i
C. 6-4i
D. 12+4i
Đáp án A.
Do ![]() nên tập hợp điểm M là các điểm nằm ngoài đường tròn
nên tập hợp điểm M là các điểm nằm ngoài đường tròn ![]() và nằm trong đường tròn
và nằm trong đường tròn 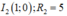
Dựa vào hình vẽ ta chứng minh được ![]()
Khi đó ![]()
Gọi T là tập hợp các số phức z thỏa mãn z - i ≥ 3 và z - 1 ≤ 5 . Gọi z 1 ; z 2 ∈ T lần lượt là các số phức có môdun nhỏ nhất và lớn nhất. Tìm số phức z 1 + 2 z 2
A. 12 + 2 i
B. - 2 + 12 i
C. 6 - 4 i
D. 12 + 4 i
Số phức z = a + bi có phần thực, phần ảo là các số nguyên và thỏa mãn: z 3 = 2 + 11 i . Giá trị biểu thức T = a + b là
A. 2
B. 3
C. 4
D. 5
Tập hợp các điểm biểu diễn số phức z thỏa mãn z ' = ( z + i ) ( z + i ) là một số thực và là đường thẳng có phương trình
A. x = 0
B. y = 0
C. x = y
D. x = -y
Phương trình \(z^2+az+b=0\) với a b là các số thực nhận số phức 1+i là một nghiệm.Tính a - b?
A:-2
B:-4
C:4
D:0
Nếu \(z_1=a+bi\) là nghiệm thì \(z_2=a-bi\) cũng là nghiệm, do đó \(1-i\) cũng là nghiệm
\(\Rightarrow\left\{{}\begin{matrix}-a=z_1+z_2=2\\b=z_1z_2=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=2\end{matrix}\right.\)
\(\Rightarrow a-b=-4\)
Trong số các số phức z thỏa mãn điều kiện z - 4 + 3 i = 3 gọi z 0 là số phức có mô đun lớn nhất. Khi đó z 0 là:
A. 3
B. 4
C. 5
D. 8
Đáp án D
Cách giải: gọi z=x+yi
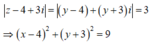
Vậy quỹ tích các điểm z thuộc đường tròn tâm I(4;-3); R=3
Đặt 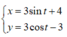
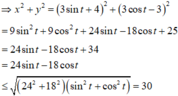
(theo bunhiacopxki)
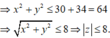
Trong số các số phức z thỏa mãn điều kiện |z-4+3i|=3, gọi z 0 là số phức có mô đun lớn nhất. Khi đó | z 0 | là:
A. 3
B. 4
C. 5
D. 8
Cho số phức \(z=1-i+i^3\) . Tìm phần thực a và phần ảo b của z:
A: a=1,b=0
B: a=0,b=1
C: a=1,b=-2
D: a=-2,b=1
\(z=1-i+i.i^2=1-i+\left(-1\right).i=1-2i\)
phần thực a=1, phần ảo b=-2
vậy chọn C
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng (Oxy) biểu diễn các số phức z và 1 + i z . Tính |z| biết diện tích tam giác OAB bằng 8.
A. |z| = 4
B. | z | = 4 2
C. |z| = 2
D. | z | = 2 2