Trong không gian cho các đường thẳng a, b, c và mặt phẳng (P). Mệnh đề nào sau đây sai?
![]()
![]()
![]()

Trong không gian cho các đường thẳng a, b, c và mặt phẳng (P). Mệnh đề nào sau đây sai?
A. Nếu a//b và b ⊥ c thì c a
B. Nếu a ⊥ b và b ⊥ c thì a//c
C. Nếu a ⊥ (P) và b//(P) thì a ⊥ b
D. Nếu a ⊥ b, c ⊥ b và a cắt c thì b vuông góc với mặt phẳng chứa a và c
Đáp án B
Phương pháp: Suy luận từng đáp án.
Cách giải: Nếu a ⊥ b và b ⊥ c thì b ⊥ (a;c) => ta không thể kết luận a//c
Trong không gian cho đường thẳng a chứa trong mặt phẳng (P) và b chứa trong mặt phẳng (Q). Mệnh đề nào sau đây là đúng?
A. P // Q ⇒ a // b .
B. a // b ⇒ P // Q .
C. P // Q ⇒ a // Q b // P .
D.a, b chéo nhau.
Trong không gian cho đường thẳng a chứa trong mặt phẳng (P) và b chứa trong mặt phẳng (Q). Mệnh đề nào sau đây là đúng?
A. P // Q ⇒ a // b .
B. a // b ⇒ P // Q .
C. P // Q ⇒ a // Q b // P .
D. a, b chéo nhau
Cho 2 đường thẳng phân biệt a và b không nằm trong mặt phẳng P , trong đó a ⊥ P . Mệnh đề nào sau đây là sai ?
A. Nếu b / / P thì b ⊥ a
B. Nếu b ⊥ P thì b cắt a
C. Nếu b ⊥ a thì b / / P
D. Nếu b / / a thì b ⊥ P
Đáp án B
Các khẳng định A, C và D sai; khẳng định B đúng.
Cho 2 đường thẳng phân biệt a và b không nằm trong mặt phẳng (P), trong đó a ⊥ ( P ) . Mệnh đề nào sau đây là sai ?
![]()
![]()
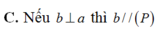
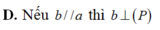
Đáp án B
Các khẳng định A, C và D sai; khẳng định B đúng.
Cho 2 đường thẳng phân biệt a và b không nằm trong mặt phẳng ( P ) , trong đó a ⊥ ( P ) . Mệnh đề nào sau đây là sai ?
![]()
![]()
![]()
![]()
Đáp án B
Các khẳng định A, C và D sai;
khẳng định B đúng.
Trong không gian cho hai đường thẳng a và b cắt nhau. Đường thẳng c cắt cả hai đường a và b. Có bao nhiêu mệnh đề sai trong các mệnh đề sau
(I) a, b, c luôn đồng phẳng
(II) a, b đồng phẳng
(III) a, c đồng phẳng
A. 0
B. 1
C. 2
D. 3
Trong không gian cho hai đường thẳng a và b cắt nhau. Đường thẳng c cắt cả hai đường a và b. Có bao nhiêu mệnh đề sai trong các mệnh đề sau
(I) a, b, c luôn đồng phẳng
(II) a, b đồng phẳng
(III) a, c đồng phẳng
A. 0
B. 1
C. 2
D. 3
Xét các mệnh đề sau đây xem mệnh đề nào đúng, mệnh đề nào sai ?
a) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước
b) Qua một đường thẳng, có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước
c) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước
d) Cho hai đường thẳng a và b. Nếu có mặt phẳng \(\left(\alpha\right)\) không chứa cả a và b thì a và b chéo nhau