Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : 2 x - 2 y + z - 3 = 0 và điểm M(1;-2;13). Tính khoảng cách từ điểm M đến mặt phẳng (a).
![]()
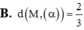
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): x+y+z-6=0. Điểm nào dưới đây không thuộc mặt phẳng (α)?
A. M(1; -1; 1)
B. Q(3; 3; 0)
C. N(2; 2; 2)
D. P(1; 2; 3).
Đáp án A
Ta có 1+(-1)+1-6 ≠ 0
=> Tọa độ điểm M không thỏa mãn phương trình mặt phẳng (α) nên điểm M không thuộc mặt phẳng (α).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( α ) : x + y + z - 6 = 0 . Điểm nào dưới đây không thuộc mặt phẳng ( α ) ?
A. P(1;2;3)
B. Q(3;3;0)
C. M(1;-1;1)
D. N(2;2;2)
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng α : x + y - z + 1 = 0 v à β : - 2 x + m y + 2 z - 2 = 0 . Tìm m để mặt phẳng (α) song song với mặt phẳng (β).
A. m = 2
B. m = 5
C. Không tồn tại
D. m = -2
Trong không gian với hệ tọa độ Oxyz cho điểm M(1;4;2) và mặt phẳng ( α ) : x + y + z - 1 = 0 . Tọa độ điểm M’ đối xứng với điểm M qua mặt phẳng (α) là
A. M’(0;-2;-3)
B. M’(-3;-2;0)
C. M’(-2;0;-3)
D. M’(-3;0;-2)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( α ): x+y+z-6=0 . Điểm nào dưới đây không thuộc ( α ) ?
A. N(2;2;2)
B. Q(3;3;0)
C. P(1;2;3)
D. M(1;-1;1)
Đáp án D
Dễ thấy tọa độ M(1;-1;1) không thỏa mãn phương trình mặt phẳng ( α )
Trong không gian với hệ tọa độ Oxyz, cho α là mặt phẳng chứa hai đường thẳng d 1 : x − 1 3 = y + 2 − 1 = z + 1 2 và d 2 : x = 12 − 3 t y = t z = 10 − 2 t . Phương trình mặt phẳng α là
A. 15 x − 11 y − 17 z − 54 = 0 .
B. 15 x + 11 y − 17 z + 10 = 0 .
C. 15 x − 11 y − 17 z − 24 = 0.
D. 15 x + 11 y − 17 z − 10 = 0 .
Đáp án D
Đường thẳng d 1 đi qua M 1 1 ; − 2 ; − 1 và có VTCP u 1 → = 3 ; − 1 ; 2 .
Đường thẳng d 2 đi qua M 2 12 ; 0 ; 10 và có VTCP u 2 → = − 3 ; 1 ; − 2 .
Như vậy: u 1 → = − u 2 → , M 1 ∉ d 2 . Suy ra d 1 / / d 2 .
Chú ý: Hai đường thẳng d 1 và d 2 song song nên em không thể lấy tích có hướng của hai VTCP để tìm VTPT của mặt phẳng vì tích có hướng của hai vectơ cùng phương là vectơ-không.
Gọi n → là một VTPT của mặt phẳng α thì vuông n → góc với hai vectơ không cùng phương

Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;4;2) và mặt phẳng α : x+y+z-1=0 Tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng α là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;4;2) và mặt phẳng α : x + y + z - 1 = 0 . Tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng α là:
A. (2;-1;0)
B. (-1;2;0)
C. (-1;0;2)
D. (0;-1;2)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : 3x-2y+z+6=0. Hình chiếu vuông góc của điểm A(2;-1;0) lên mặt phẳng α có tọa độ là
A. (1;0;3)
B. (-1;1;-1)
C. (2;-2;3)
D. (1;1;-1)
Đáp án B
Phương pháp giải: Viết phương trình đường thẳng vuông góc với mặt và đi qua điểm, tọa độ giao điểm của đường thẳng và mặt phẳng chính là tọa độ hình chiếu của điểm
Lời giải:
Gọi H là hình chiếu của A trên α
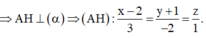
![]()
![]()
![]()
=> t= - 1
Vậy tọa độ điểm cần tìm là H(-1;1;-1)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): 3x – 2y + z + 6 = 0. Hình chiếu vuông góc của điểm A(2; –1;0) lên mặt phẳng (α) có tọa độ là
A. (1;0;3)
B. (–1;1;–1)
C. (2;–2;3)
D. (1;1;–1)
Đáp án B
Phương pháp giải: Viết phương trình đường thẳng vuông góc với mặt và đi qua điểm, tọa độ giao điểm của đường thẳng và mặt phẳng chính là tọa độ hình chiếu của điểm
Lời giải:
Gọi H là hình chiếu của A trên 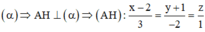
Vì ![]()
mà ![]()
Vậy tọa độ điểm cần tìm là H (–1;1;–1)