Vẽ hình khai triển (cắt theo các cạnh B 1 C 1 , C B 1 , C 1 A 1 ,CA) của lăng trụ đứng đáy tam giác có các kích thước cho như hình bên với a = 5cm, c = 4,2cm, hc = 4cm, h = 3,8cm
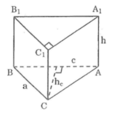
Cắt và gấp một miếng bìa thành hình lăng trụ tam giác theo hướng dẫn sau:
Bước 1: Vẽ hình khai triển theo mẫu và cắt theo viền (H. 10.22)
Bước 2: Gấp theo nét màu cam. Ta được hình lăng trụ (H. 10.23)
Học sinh thực hiện theo hướng dẫn.
Vẽ hình khai triển (cắt theo các cạnh \(B_1C_1,C_1C,CB\) và \(C_1A_1,CA\)) của lăng trụ đứng, đáy tam giác, có các kích thước cho như hình 125 với \(a=5cm,c=4,2cm,h_c=4cm,h=3,8cm\)
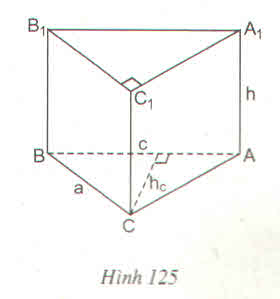
Sử dụng bìa cứng và gấp chiếc hộp có dạng hình hộp chữ nhật với kích thước như hình 10.3 theo hướng dẫn sau:
Bước 1: Vẽ hình khai triển của hình hộp chữ nhật theo kích thước đã cho như Hình 10.4.
Bước 2: Cắt theo viền
Bước 3: Gấp theo đường màu cam để được hình hộp chữ nhật (H.10.5)
Bước 1: Vẽ hình khai triển của hình hộp chữ nhật theo kích thước đã cho như Hình 10.4.
Bước 2: Cắt theo viền
Bước 3: Gấp theo đường màu cam để được hình hộp chữ nhật (H.10.5)
Quan sát các hình khai triển trên hình vẽ dưới rồi cho biết: Cạnh nào sẽ được ghép với cạnh AB để được hình lăng trụ đứng (sử dụng các số cho trên hình)
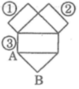
Có 5 mặt ghép thành lăng trụ đứng là tam giác có cạnh là AB nên cạnh số 1 ghép với cạnh AB ta sẽ được lăng trụ đứng
Quan sát các hình khai triển trên hình vẽ dưới rồi cho biết: Cạnh nào sẽ được ghép với cạnh AB để được hình lăng trụ đứng (sử dụng các số cho trên hình)
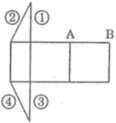
Có 5 mặt ghép thành lăng trụ đứng có đáy là tam giác thì cạnh 2 sẽ được ghép với cạnh AB ta sẽ được lăng trụ đứng
Vẽ lên một miếng bìa hình khai triển của hình hộp chữ nhật (tương tự hình bên) với kích thước tùy chọn. Cắt rời hình đã vẽ rồi gấp theo đường màu cam để được một hình hộp chữ nhật.
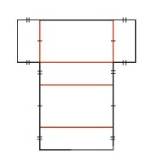
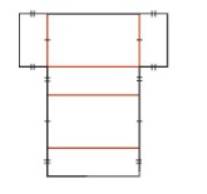
Cắt và gấp theo đường màu cam.
Từ một hình trụ, cắt rời 2 đáy và cắt dọc theo đường sinh AB của mặt xung quanh rồi trải thẳng ra, ta được hình khai triển mặt xung quanh của hình trụ là một hình chữ nhật có một cạnh bằng chu vi hình tròn đáy, cạnh còn lại bằng chiều cao của hình trụ.
Hãy vẽ sơ đồ hình cây của khai triển \({(a + b)^4}\) được mô tả như Hình 8.9. Sau khi khai triển, ta thu được một tổng gồm \({2^4}\) (theo quy tắc nhân) đơn thức có dạng x. y. z. t, trong đó mỗi x, y, z, t là a hoặc b. Chẳng hạn, nếu x, y, t là a, còn z là b thì ta có đơn thức a. a. b. a, thu gọn là \({a^3}b\). Để có đơn thức này, thì trong 4 nhân tử x, y, z, t có 1 nhân tử là b, 3 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với \({a^3}b\) trong tổng là \(C_4^1\).
Lập luận tương tự trên, dùng kiến thức về tổ hợp, hãy cho biết trong tổng nêu trên, có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau.
\({a^4};\quad {a^3}b;\quad {a^2}{b^2};\quad a{b^3};\quad {b^4}?\)
Số đơn thức đồng dạng với \({a^4}\) trong tổng là \(C_4^0 = 1\)
Số đơn thức đồng dạng với \({a^3}b\) trong tổng là \(C_4^4 = 1\)
Số đơn thức đồng dạng với \({a^2}{b^2}\) trong tổng là \(C_4^2 = 6\)
Số đơn thức đồng dạng với \(a{b^3}\) trong tổng là \(C_4^3 = 1\)
Số đơn thức đồng dạng với \({b^4}\) trong tổng là \(C_4^4 = 1\)
Dùng kéo cắt một tờ giấy thành hình tam giác ABC. Đặt tam giác lên tờ giấy thứ hai. Vẽ và cắt theo các cạnh của tam giác ABC thành tam giác A’B’C’ (Hình 1). Hãy so sánh các cạnh và các góc của hai tam giác ABC và A’B’C’.
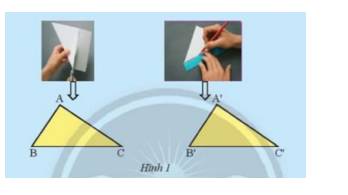
Ta thấy 2 tam giác có các cặp góc bằng nhau \(\widehat A = \widehat {A'}\); \(\widehat B = \widehat {B'}\); \(\widehat C = \widehat {C'}\)
2 tam giác có các cặp cạnh bằng nhau AC = A’C’; AB = A’B’; BC = B’C’