z - 3 + 4 i = 2 , w = 2 z + 1 - i Khi đó |w| có giá trị lớn nhất là:
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn (3 + 2i)z + (2 - i)2 = 4 + i. Môđun của số phức w = ( z + 1 ) z là
A. 2
B. 4
C. 10
D. 10
\(M\left(1;1\right)\) ; \(N\left(2;3\right)\)
Gọi \(w=x+yi\Rightarrow Q\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;2\right)\\\overrightarrow{MQ}=\left(x-1;y-1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MN}+3\overrightarrow{MQ}=\left(3x-2;3y-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow w=\dfrac{2}{3}+\dfrac{1}{3}i\)
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Xét các số phức w,z thỏa mãn | w + i | = 3 5 5 và 5 w = ( 2 + i ) ( z - 4 ) . Tìm giá trị lớn nhất của biểu thức P = | z - 2 i | + | z - 6 - 2 i |
A. 7.
B . 2 53 .
C . 2 58 .
D . 4 13 .
Cho các số phức w,z thỏa mãn w + i = 3 5 5 và 5w=(2+i)(z-4).
Giá trị lớn nhất của biểu thức P = z - 1 - 2 i + z - 5 - 2 i bằng
A. 6 7
B. 4 + 2 13
C. 2 53
D. 4 13
Đáp án C
HD: Ta có
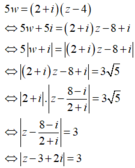
![]() Tập hợp điểm M(z) là đường tròn
Tập hợp điểm M(z) là đường tròn ![]() tâm I(3;-2), R=3.
tâm I(3;-2), R=3.
Gọi A(1;2), B(5;2) và E(3;2) là trung điểm của AB suy ra P=MA+MB
Lại có
![]()
![]() P lớn nhất
P lớn nhất  ME lớn nhất.
ME lớn nhất.
Mà ![]()
Vậy ![]()
Cho các số phức w, z thỏa mãn w + i = 3 5 5 và 5 w = ( 2 + i ) ( z - 4 ) . Giá trị lớn nhất của biểu thức P = z - 1 - 2 i + z - 5 - 2 i bằng
![]()
![]()
![]()
![]()
Cho hai số phức z, w thỏa mãn | z - 3 - 2 i | ≤ 1 | w + 1 + 2 i | ≤ | w - 2 - i | . Tìm gía trị nhỏ nhất P m i n của biểu thức P = |z-w|.
A . P m i n = 3 2 - 2 2
B . P m i n = 2 + 1
C . P m i n = 5 2 - 2 2
D . P m i n = 2 2 + 1 2
Các số phức z, w thay đổi nhưng thỏa mãn |z + i – 2i| = 1 và |w - 3 + i| = 3. Tìm |z - w|max
A. |z - w|max = 2.
B. |z - w|max = 4.
C. |z - w|max = 9.
D. |z - w|max = 10.