Cho hàm số y = f x = e a x - e 3 x 2 x k h i x ≠ 0 1 2 k h i x = 0 . Tìm giá trị của a để hàm số f(x) liên tục tại điểm x = 0.
A. a = 2
B. a = 4
C. a = - 1 4
D. a = - 1 2
Những câu hỏi liên quan
Cho hàm số y f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y f( x) trên [ a; e]? A.
m
a
x
[
a
,...
Đọc tiếp
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x) trên [ a; e]?
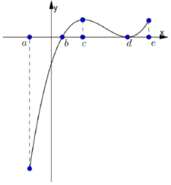
A. m a x [ a , e ] f ( x ) = f ( c ) m i n [ a , e ] f ( x ) = f ( a )
B. m a x [ a , e ] f ( x ) = f ( a ) m i n [ a , e ] f ( x ) = f ( b )
C. m a x [ a , e ] f ( x ) = f ( e ) m i n [ a , e ] f ( x ) = f ( b )
D. m a x [ a , e ] f ( x ) = f ( d ) m i n [ a , e ] f ( x ) = f ( b )
Ta có bảng biến thiên như hình vẽ sau:
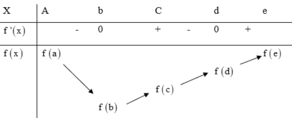
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
;
m
)
có đồ thị hàm số
y
f
(
x
;
m
)
như hình vẽ Biết
f
(
a
)
f
(
c
)
0
;
f
(
b
)
0
f
(
e
)
Hỏi hàm số...
Đọc tiếp
Cho hàm số y = f ( x ; m ) có đồ thị hàm số y = f ' ( x ; m ) như hình vẽ
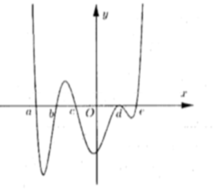
Biết f ( a ) > f ( c ) > 0 ; f ( b ) < 0 < f ( e ) Hỏi hàm số y = f ( x , m ) có bao nhiêu điểm cực trị?
A. 5
B. 7
C. 9
D. 10
Cho hàm số y f( x) ax4+ bx3+ cx2+ dx+ e với a ≠0. Biết rằng hàm số y f( x) có đạo hàm là f’(x) và hàm số y f’(x) có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai? A. Trên khoảng (-2; 1) thì hàm số y f( x) luôn tăng. B. Hàm số y f(x) giảm trên đoạn [ -1; 1] . C. Hàm số y f( x) đồng biến trên khoảng (1+ ∞) . D. Hàm số y f( x) nghịch biến trên khoảng (- ∞; -2)
Đọc tiếp
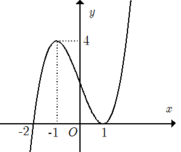
Cho hàm số y= f( x) = ax4+ bx3+ cx2+ dx+ e với a ≠0. Biết rằng hàm số y= f( x) có đạo hàm là f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai?
A. Trên khoảng (-2; 1) thì hàm số y= f( x) luôn tăng.
B. Hàm số y= f(x) giảm trên đoạn [ -1; 1] .
C. Hàm số y= f( x) đồng biến trên khoảng (1+ ∞) .
D. Hàm số y= f( x) nghịch biến trên khoảng (- ∞; -2)
Chọn C
Trên đoạn [ - 1; 1] đồ thị hàm số y= f’( x) nằm phía trên trục hoành.
=> Trên đoạn [ - 1; 1] thì f’( x) > 0.
=> Trên đoạn [ - 1; 1] thì hàm số y= f( x) đồng biến
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
,
(
a
,
b
,
c
,
d
,
e
∈
ℝ
)
Hàm yf(x) có bảng xét dấu như sau: Số nghiệm của phương trình f(x)e là A....
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e , ( a , b , c , d , e ∈ ℝ ) Hàm y=f'(x) có bảng xét dấu như sau:
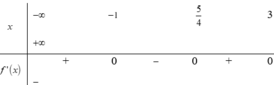
Số nghiệm của phương trình f(x)=e là
A. 1
B. 0
C. 2
D. 3
. a) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f( 1 2 ); f( 1 2 ). b) Cho hàm số y = g(x) = x 2 – 1. Tính g(-1); g(0
giúp e với ạ
a: f(-2)=4+3=7
f(-1)=2+3=5
f(0)=3
f(1/2)=-1+3=2
f(-1/2)=1+3=4
b: g(-1)=1-1=0
f(0)=0-1=-1
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
3
+
d
x
+
e
(
a
≠
0
)
. Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số yf’(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai? A. Hàm số f(x) nghịch biến trên khoảng (-1;1...
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 3 + d x + e ( a ≠ 0 ) . Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số y=f’(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai?
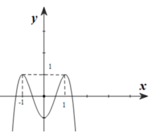
A. Hàm số f(x) nghịch biến trên khoảng (-1;1)
B. Hàm số f(x) đồng biến trên khoảng (0;+∞)
C. Hàm số f(x) đồng biến trên khoảng (-2;1)
D. Hàm số f(x) nghịch biến trên khoảng (-∞;-2)
Chọn A
Phương pháp:
Nếu f ' ( x ) ≥ 0 , ∀ x ∈ a ; b và chỉ bằng 0 tại hữu hạn điểm trên đó thì f(x) đồng biến trên khoảng (a;b).
Nếu f ' ( x ) ≤ 0 , ∀ x ∈ a ; b và chỉ bằng 0 tại hữu hạn điểm trên đó thì f(x) nghịch biến trên khoảng (a;b) Cách giải:
Quan sát đồ thị hàm số y=f’(x) , ta thấy f’(x) >0 =>Hàm số f (x) đồng biến trên
khoảng (-1;1).
=>Mệnh đề ở câu A là sai.
Đúng 0
Bình luận (0)
Cho hàm số y f( x) ax4+ bx3+ cx2+ dx+ e với a≠0. Đồ thị hàm số y f’(x) như hình bên. Khẳng định nào sau đây sai? A. Hàm số y f(x) đồng biến trên ( -2; 1) B. Hàm số y f( x) đồng biến trên (1; + ∞) C. Hàm số y f(x) nghịch biến trên đoạn có độ dài nhỏ hơn 1000. D. Hàm số y f( x) nghịch biến trên (- ∞; -2)
Đọc tiếp
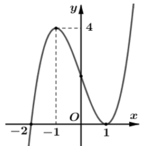
Cho hàm số y= f( x) = ax4+ bx3+ cx2+ dx+ e với a≠0. Đồ thị hàm số y= f’(x) như hình bên. Khẳng định nào sau đây sai?
A. Hàm số y= f(x) đồng biến trên ( -2; 1)
B. Hàm số y= f( x) đồng biến trên (1; + ∞)
C. Hàm số y= f(x) nghịch biến trên đoạn có độ dài nhỏ hơn 1000.
D. Hàm số y= f( x) nghịch biến trên (- ∞; -2)
Chọn C
Dựa vào đồ thị của hàm số y= f’(x) ta thấy:
+ f’(x) > 0 khi x ∈ (-2;1) ∪ (1; + ∞)
=> Hàm số y= f(x) đồng biến trên các khoảng ( -2; 1) và ( 1; + ∞).
Suy ra A đúng, B đúng.
+ Ta thấy : f’(x)< 0 khi x< -2 ( chú ý nhận dạng đồ thị của hàm số bậc ba)
=> Hàm số y= f( x) nghịch biến trên khoảng ( - ∞; -2) .
Suy ra D đúng.
+ Dùng phương pháp loại trừ, ta chọn C
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục, có đạo hàm trên [-1;0]. Biết f’(x) (3x2+2x)e-f(x)
∀
x
∈
-
1
;
0
Tính giá trị biểu thức Af(0)-f(-1)
Đọc tiếp
Cho hàm số y=f(x) liên tục, có đạo hàm trên [-1;0]. Biết f’(x) = (3x2+2x)e-f(x) ∀ x ∈ - 1 ; 0 Tính giá trị biểu thức A=f(0)-f(-1)
Cho hàm số
f
x
a
x
4
+
b
x
3
+
c
x
3
+
d
x
+
e
a
≠
0
. Biết rằng hàm số f(x) có đạo hàm là f(x) và hàm số yf(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai? A. Hàm số...
Đọc tiếp
Cho hàm số f x = a x 4 + b x 3 + c x 3 + d x + e a ≠ 0 . Biết rằng hàm số f(x) có đạo hàm là f'(x) và hàm số y=f'(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai?
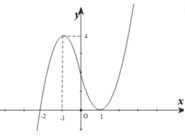
A. Hàm số f(x) nghịch biến trên khoảng (-1;1)
B. Hàm số f(x) đồng biến trên khoảng 0 ; + ∞
C. Hàm số f(x) đồng biến trên khoảng (-2;1)
D. Hàm số f(x) nghịch biến trên khoảng - ∞ ; - 2
Cho hàm số f(x)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
, với a,b,c,d,e
∈
ℝ
. Hàm số y f(x) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng? A. a + b + c + d 0. B. a + c b + d C. a + c 0 D. d + b - c 0
Đọc tiếp
Cho hàm số f(x) = a x 4 + b x 3 + c x 2 + d x + e , với a,b,c,d,e ∈ ℝ . Hàm số y = f'(x) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
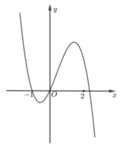
A. a + b + c + d < 0.
B. a + c < b + d
C. a + c > 0
D. d + b - c > 0
Chọn C
Ta có: 
Dựa vào đồ thị:
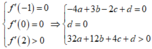
Dựa vào đồ thị, ta cũng có: 
Từ (1),(2) suy ra a + c > 4a + c > 0.
Đúng 0
Bình luận (0)