M=y=-3/x có tung độ là 3

<=>y=3

khi đó y=-3/x<=>3=-3/x

<=>3x=-3<=>x=-1

Vậy hoành độ của M=-1

a: Bạn bổ sung đề đi bạn

b: thay x=-3 và y=0 vào (d), ta được:

\(-3\left(2m+1\right)-m+3=0\)

=>-6m-3-m+3=0

=>-7m=0

=>m=0

d: y=(2m+1)x-m+3

=2mx+x-m+3

=m(2x-1)+x+3

Tọa độ điểm cố định mà (1) luôn đi qua là:

\(\left\{{}\begin{matrix}2x-1=0\\y=x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=3+\dfrac{1}{2}=\dfrac{7}{2}\end{matrix}\right.\)

a: Thay x=-1 và y=2 vào (d), ta được:

\(-\left(m-2\right)+n=2\)

=>-m+2+n=2

=>-m+n=0

=>m-n=0(1)

Thay x=3 và y=-4 vào (d), ta được:

\(3\left(m-2\right)+n=-4\)

=>3m-6+n=-4

=>3m+n=2(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}m-n=0\\3m+n=2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m-n+3m+n=2\\m-n=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4m=2\\n=m\end{matrix}\right.\Leftrightarrow n=m=\dfrac{1}{2}\)

b: Thay x=0 và \(y=1-\sqrt{2}\) vào (d), ta được:

\(0\left(m-2\right)+n=1-\sqrt{2}\)

=>\(n=1-\sqrt{2}\)

Vậy: (d): \(y=\left(m-2\right)x+1-\sqrt{2}\)

Thay \(x=2+\sqrt{2}\) và y=0 vào (d), ta được:

\(\left(m-2\right)\cdot\left(2+\sqrt{2}\right)+1-\sqrt{2}=0\)

=>\(\left(m-2\right)\left(2+\sqrt{2}\right)=\sqrt{2}-1\)

=>\(m-2=\dfrac{\sqrt{2}-1}{2+\sqrt{2}}=\dfrac{-4+3\sqrt{2}}{2}\)

=>\(m=\dfrac{-4+3\sqrt{2}+4}{2}=\dfrac{3\sqrt{2}}{2}\)

c: 2y+x-3=0

=>2y=-x+3

=>\(y=-\dfrac{1}{2}x+\dfrac{3}{2}\)

Để (d) vuông góc với đường thẳng y=-1/2x+3/2 thì

\(-\dfrac{1}{2}\left(m-2\right)=-1\)

=>m-2=2

=>m=4

Vậy: (d): \(y=\left(4-2\right)x+n=2x+n\)

Thay x=1 và y=3 vào y=2x+n, ta được:

\(n+2\cdot1=3\)

=>n+2=3

=>n=1

d: 3x+2y=1

=>\(2y=-3x+1\)

=>\(y=-\dfrac{3}{2}x+\dfrac{1}{2}\)

Để (d) song song với đường thẳng \(y=-\dfrac{3}{2}x+\dfrac{1}{2}\) thì

\(\left\{{}\begin{matrix}m-2=-\dfrac{3}{2}\\n\ne\dfrac{1}{2}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m=\dfrac{1}{2}\\n\ne\dfrac{1}{2}\end{matrix}\right.\)

Vậy: (d): \(y=\left(\dfrac{1}{2}-2\right)x+n=-\dfrac{3}{2}x+n\)

Thay x=1 và y=2 vào (d), ta được:

\(n-\dfrac{3}{2}=2\)

=>\(n=2+\dfrac{3}{2}=\dfrac{7}{2}\left(nhận\right)\)

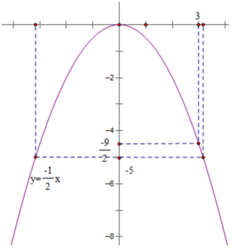
a) Từ đồ thị, ta xác định được tung độ của điểm D là (-9)/2

Với x = 3 ta có:  y   =   ( - 1 ) / 2   x 2   =   ( - 1 ) / 2 . 3 2   =   ( - 9 ) / 2

Hai kết quả là như nhau.

b) Có 2 điểm có tung độ bằng -5

Giá trị của hoành độ của hai điểm lần lượt là ≈ -3,2 và ≈ 3,2

a: Thay x=0 và y=2 vào (d), ta được:

\(0\left(m-1\right)+m=2\)

=>m+0=2

=>m=2

b: Thay x=-3 vào y=0 vào (d), ta được:

\(-3\left(m-1\right)+m=0\)

=>-3m+3+m=0

=>-2m+3=0

=>-2m=-3

=>\(m=\dfrac{3}{2}\)

c: Khi m=2 thì (d): \(y=\left(2-1\right)x+2=x+2\)

Khi m=3/2 thì (d): \(y=\left(\dfrac{3}{2}-1\right)x+\dfrac{3}{2}=\dfrac{1}{2}x+\dfrac{3}{2}\)

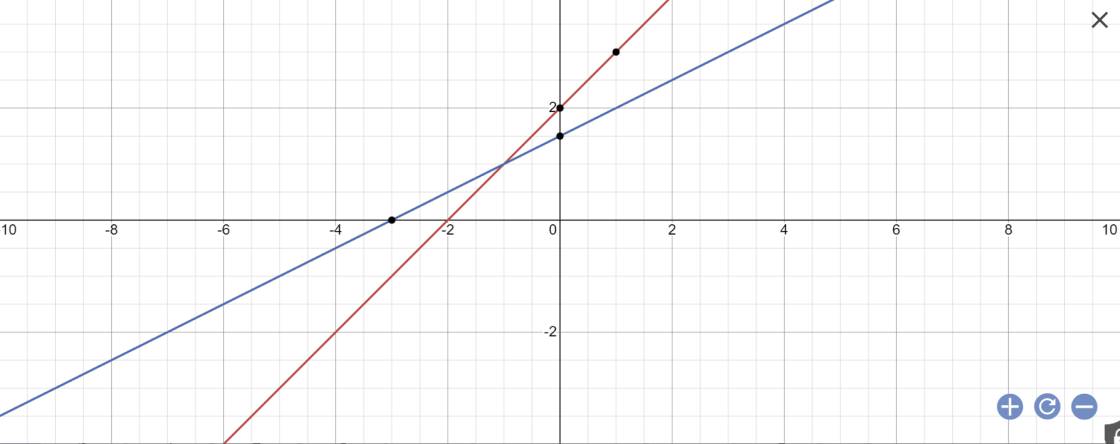
Tọa độ giao điểm của hai đường thẳng này là nghiệm của hệ phương trình sau:

\(\left\{{}\begin{matrix}x+2=\dfrac{1}{2}x+\dfrac{3}{2}\\y=x+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x-\dfrac{1}{2}x=\dfrac{3}{2}-2\\y=x+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{1}{2}x=-\dfrac{1}{2}\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-1+2=1\end{matrix}\right.\)

1: Để hàm số đồng biến thì m-3>0

hay m>3

2: Thay x=0 và y=0 vào (d), ta được:

3m+7=0

hay \(m=-\dfrac{7}{3}\)