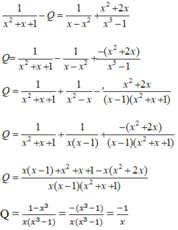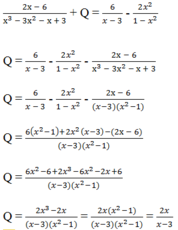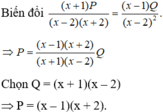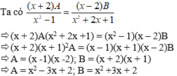Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức: x + 2 . P x 2 - 1 = x - 2 . Q x 2 - 2 x + 1

Những câu hỏi liên quan
Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức :
x
+
2
P
x
-
2
x
-
1
Q
x
2...
Đọc tiếp
Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức : x + 2 P x - 2 = x - 1 Q x 2 - 4
x + 2 P x - 2 = x - 1 Q x 2 - 4
⇒ x + 2 . P . x 2 - 4 = x - 2 x - 1 . Q
Hay (x + 2)(x – 2)(x + 2).P = (x – 2)(x – 1).Q
Chọn P = (x – 1) thì Q = x + 2 2
Đúng 0
Bình luận (0)
Trong mỗi trường hợp sau đây, hãy tìm hai đa thức P và Q thỏa mãn đẳng thức :
a) \(\dfrac{\left(x+2\right)P}{x-2}=\dfrac{\left(x-1\right)Q}{x^2-4}\)
b) \(\dfrac{\left(x+2\right)P}{x^2-1}=\dfrac{\left(x-2\right)Q}{x^2-2x+1}\)
a) \(\dfrac{\left(x+2\right)P}{x-2}=\dfrac{\left(x-1\right)Q}{x^2-4}\)
\(\Leftrightarrow\left(x^2-4\right)\left(x+2\right)P=\left(x-2\right)\left(x-1\right)Q\)
\(\Leftrightarrow\)\(\left(x+2\right)^2\left(x-2\right)P=\left(x-2\right)\left(x-1\right)Q\)
\(\Leftrightarrow\)\(\left(x+2\right)^2P=\left(x-1\right)Q\)
\(\Leftrightarrow P=x-1\)
\(Q=\left(x+2\right)^2=x^2+4x+4\)
b)\(\dfrac{\left(x+2\right)P}{x^2-1}=\dfrac{\left(x-2\right)Q}{x^2-2x+1}\)
\(\Leftrightarrow\left(x-1\right)^2\left(x+2\right)P=\left(x+1\right)\left(x-1\right)\left(x-2\right)Q\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)P=\left(x+1\right)\left(x-2\right)Q\)
\(\Leftrightarrow P=\left(x+1\right)\left(x-2\right)=x^2-x-2\)
\(Q=\left(x-1\right)\left(x+2\right)=x^2+x-2\)
Đúng 0
Bình luận (0)
Trong mỗi trường hợp sau hãy tìm 2 đa thức P và đa thức Q thỏa mãn đẳng thức :a) frac{left(x+2right)P}{x-2}frac{left(x-1right)Q}{x^2-4};b) frac{left(x+2right)P}{x^2-1}frac{left(x-2right)Q}{x^2-2x+1}.Cô ơi, cô đừng giải bài này mà hướng dẫn chi tiết phương pháp để tìm P và Q trong 2 theo từng câu a) và câu b) giúp em nhe cô. Em cám ơn cô nhìu nhìu ạ, hihi :)
Đọc tiếp
Trong mỗi trường hợp sau hãy tìm 2 đa thức P và đa thức Q thỏa mãn đẳng thức :
a) \(\frac{\left(x+2\right)P}{x-2}=\frac{\left(x-1\right)Q}{x^2-4};\)
b) \(\frac{\left(x+2\right)P}{x^2-1}=\frac{\left(x-2\right)Q}{x^2-2x+1}.\)
Cô ơi, cô đừng giải bài này mà hướng dẫn chi tiết phương pháp để tìm P và Q trong 2 theo từng câu a) và câu b) giúp em nhe cô. Em cám ơn cô nhìu nhìu ạ, hihi :)
a)\(\frac{\left(x+2\right)P}{x-2}=\frac{\left(x+2\right)^2P}{\left(x-2\right)\left(x+2\right)}=\frac{\left(x+2\right)^2P}{x^2-4}=\frac{\left(x-1\right)Q}{x^2-4}\Rightarrow\left(x+2\right)^2P=\left(x-1\right)Q\)
\(\Rightarrow\frac{P}{Q}=\frac{x-1}{\left(x+2\right)^2}\)
b) Từ gt,ta có :\(\left(x+2\right)\left(x^2-2x+1\right)P=\left(x^2-1\right)\left(x-2\right)Q\)
\(\Leftrightarrow\left(x+2\right)\left(x-1\right)^2P=\left(x-1\right)\left(x+1\right)\left(x-2\right)Q\)
\(\Leftrightarrow\left(x+2\right)\left(x-1\right)P=\left(x+1\right)\left(x-2\right)Q\)
\(\Rightarrow\frac{P}{Q}=\frac{\left(x+1\right)\left(x-2\right)}{\left(x+2\right)\left(x-1\right)}=\frac{x^2-x-2}{x^2+x-2}\)
Ở đây có nhiều cặp đa thức (P ; Q) thỏa mãn lắm ! Mình xét P/Q để chỉ rằng chúng tỉ lệ với 2 đa thức ở vế phải
Ví dụ : Câu a : P = 2 - 2x thì Q = -2x2 - 8x - 8
Đúng 0
Bình luận (0)
quy đồng 2 phân thức ở 2 bên dấu "=" => tử bằng nhau (có dạng A*P = B*Q) => A=Q; B=P (trường hợp A hoặc B hoặc cả A và B là tích của 2 đa thức thì triển khai tích đó thành đa thức)
Đúng 0
Bình luận (0)
Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện :
1
x
2
+
x
+
1
-
Q
1
x
-
x
2
+
x
2
+...
Đọc tiếp
Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện : 1 x 2 + x + 1 - Q = 1 x - x 2 + x 2 + 2 x x 3 + 1
Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện:
2
x
-
6
x
3
-
3
x
2
-
x
+
3
+
Q
6
x
-...
Đọc tiếp
Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện: 2 x - 6 x 3 - 3 x 2 - x + 3 + Q = 6 x - 3 - 2 x 2 1 - x 2
Tìm đa thức thích hợp điền vào các chỗ trống thỏa mãn mỗi đẳng thức sau:a)
x
2
+
8
2
x
−
1
2
x
3
+
16
x
.
.....
Đọc tiếp
Tìm đa thức thích hợp điền vào các chỗ trống thỏa mãn mỗi đẳng thức sau:
a) x 2 + 8 2 x − 1 = 2 x 3 + 16 x . .. với x ≠ 0 và x ≠ 1 2 ;
b) . .. x − y = 2 x 2 − 2 xy 2 ( y − x ) 2 với x ≠ y .
Tìm đa thức N thỏa mãn mỗi đẳng thức sau:a)
x
+
1
N
x
2
−
2
x
+
4
x
3
+
8
với
x
≠
−
1
và ...
Đọc tiếp
Tìm đa thức N thỏa mãn mỗi đẳng thức sau:
a) x + 1 N = x 2 − 2 x + 4 x 3 + 8 với x ≠ − 1 và x ≠ − 2
b) ( x − 3 ) N 3 + x = 2 x 3 − 8 x 2 − 6 x + 36 2 + x với x ≠ ± 3 và x ≠ − 2 .
a) Kết quả N = (x + 1)(x + 2);
b) Kết quả N = 2(x + 3)(x - 3).
Đúng 0
Bình luận (0)
Tìm một cặp đa thức P và Q thỏa mãn đẳng thức:
(
x
+
1
)
P
x
2
−
4
(
x
−
1
)
Q
x
2...
Đọc tiếp
Tìm một cặp đa thức P và Q thỏa mãn đẳng thức:
( x + 1 ) P x 2 − 4 = ( x − 1 ) Q x 2 − 4 x + 4 với x ≠ ± 2 .
Tìm 1 cặp đa thức A và B thỏa mãn đẳng thức sau:
(
x
+
2
)
A
x
2
-
1
(
x
-
2
)
B
x
2
+
2
x
+...
Đọc tiếp
Tìm 1 cặp đa thức A và B thỏa mãn đẳng thức sau: ( x + 2 ) A x 2 - 1 = ( x - 2 ) B x 2 + 2 x + 1