Cho hàm số y = x 2 + x + 2 x - 1  Tập nghiệm của bất phương trình y’ < 0 là

A. [-1;3]

B. [-1;3] \ {1}

C. (-1;3)\{1}

D. (-1;3)

Cho hàm số y = x 2 + x + 2 x - 1 . Tập nghiệm của bất phương trình y’ < 0 là

A. [-1;3]

B. [-1;3] \ {1}

C. (-1;3)\{1}

D. (-1;3)

Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x )   .

Tập nghiệm của bất phương trình

f ( a - 1 ) + f ( ln a ) ≤ 0 là:

Cho hai hàm số \(f\left( x \right) = 2{{\rm{x}}^3} - {x^2} + 3\) và \(g\left( x \right) = {x^3} + \frac{{{x^2}}}{2} - 5\). Bất phương trình \(f'\left( x \right) > g'\left( x \right)\) có tập nghiệm là

A. \(\left( { - \infty ;0} \right] \cup \left[ {1; + \infty } \right)\).         

B. \(\left( {0;1} \right)\).

C. \(\left[ {0;1} \right]\).                                

D. \(\left( { - \infty ;0} \right) \cup \left( {1; + \infty } \right)\).

Cho hàm số f(x)=-1/3x³ + 4x²-7x+2. Tập nghiệm của bất phương trình: f ' ( x ) ≥ 0  là

Cho các mệnh đề sau đây:

(1) Hàm số  f ( x ) = log 2 2   x - log 2 x 4 + 4  có tập xác định  D = [ 0 ; + ∞ )

(2) Hàm số  y = log a x  có tiệm cận ngang

(3) Hàm số  y = log a x ;   0 < a < 1  và Hàm số  y = log a x ,   a > 1  đều đơn điệu trên tập xác định của nó 

(4) Bất phương trình:  log 1 2 5 - 2 x 2 - 1 ≤ 0  có 1 nghiệm nguyên thỏa mãn.

(5) Đạo hàm của hàm số  y = ln 1 - cos   x  là sin   x 1 - cos   x 2

Hỏi có bao nhiêu mệnh đề đúng:

A. 0

B. 2

C. 3

D.1

Cho hàm số f x = 3 2 x - 2 . 3 x  có đồ thị như hình vẽ sau

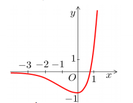
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?

(1) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại điểm có hoành độ là x = log 3 2  

(2) Bất phương trình f x ≥ - 1  có nghiệm duy nhất.

(3) Bất phương trình f x ≥ 0  có tập nghiệm là - ∞ ; log 3 2  

(4) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại 2 điểm phân biệt.

A. 2

B. 4

C. 1

D. 3

Cho hàm số f x = 3 2 x − 2.3 x  có đồ thị như hình vẽ sau

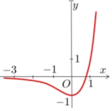
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y=0 cắt đồ thị hàm số (C) tại điểm có hoành độ là  x = log 3 2
(2) Bất phương trình f x ≥ − 1  có nghiệm duy nhất.
(3) Bất phương trình f x ≥ 0  có tập nghiệm là  − ∞ ; log 3 2
(4) Đường thẳng y=0 cát đồ thị hàm số (C) tại 2 điểm phân biệt

A. 2. 

B. 4.  

C. 1.  

D. 3.

Cho hàm số f ( x ) = 1 - 3 x + x 2 x - 1 . Tập nghiệm của bất phương trình f'(x) > 0 là:

A. R\{1}

B.  ∅

C.  1 ; + ∞

D. R