Cho số phức z = a + b i khác 0. Số phức z - 1 có phần thực là
A. a a 2 + b 2
B. - b a 2 + b 2
C. a
D. 1 a 2 + b 2
Cho số phức z = a + b i khác 0. Số phức z - 1 có phần thực là
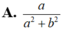
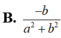
![]()
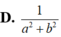
Cho số phức z thỏa mãn ( 2 − 3 i ) z + ( 4 + i ) z ¯ + ( 1 + 3 i ) 2 = 0 . Gọi a, b lần lượt là phần thực và phần ảo của số phức z. Khi đó 2 a - 3 b bằng
A. 1
B. 4
C. 11
D. -19
Cho số phức z, w khác 0 sao cho |z-w| = 2|z| = |w|. Phần thực của số phức u = z w là
A. a = - 1 8
B. a = 1 4
C. a = 1
D. a = 1 8
Đáp án D
Giả sử ![]()
Từ giả thiết đầu bài |z-w| = 2|z| = |w|, ta có hệ sau
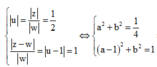
![]()
Cho số phức z, w khác 0 sao cho z − w = 2 z = w . Phần thực của số phức u = z w là
A. a = − 1 8
B. a = 1 4
C. a = 1
D. a = 1 8
Đáp án D
Giả sử u = a + b i a , b ∈ ℝ
Từ giả thiết đầu bài z − w = 2 z = w . ta có hệ sau
u = z w = 1 2 z − w w = u − 1 = 1 ⇔ a 2 + b 2 = 1 4 a − 1 2 + b 2 = 1 ⇒ a − 1 2 + a 2 = − 2 a + 1 = 3 4 ⇒ a = 1 8
Cho số phức z thỏa mãn 5 z + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a+b bằng
A. 13
B. -5
C. 9
D. 5
Cho số phức z thỏa mãn 5 z ¯ + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a + b bằng
A. 13
B. -5
C. 9
D. 5
Cho số phức z có phần thực và ảo đều khác 0. Gọi M và M’ là các điểm biểu diễn các số phức (-z) và z ¯ . Chọn khẳng định đúng.
A. M ≡ M'
B. M,M' đối xứng nhau qua Oy
C. M,M' đối xứng nhau qua O
D. M,M' đối xứng nhau qua Ox
Cho hai số phức z = a + b i và z ' = a ' + b ' i ( a , b , a ' , b ' ∈ R ) Số phức z z ' có phần thực là
![]()
![]()
![]()
![]()
Cho số phức z = ( 2 + i)( 3 - i) Tìm phần thực a và phần ảo b của số phức z ¯
A. a = 7 ; b = 1.
B. a = 7 ; b = -1.
C. a = - 7; b = 1.
D. a = -7; b = - 1.
Chọn B.
Ta có: z = ( 2 + i) ( 3 - i) = 6 - 2i + 3i - i2 = 7 + i
Nên ![]() vậy phần thực bằng a = 7 và phần ảo b = -1.
vậy phần thực bằng a = 7 và phần ảo b = -1.