Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết: x n : x 3

Những câu hỏi liên quan
Tìm n để mỗi phép chia sau là phép chia hết (n là số tự nhiên) 5 x 3 - 7 x 2 + x : 3 x n
Vì đa thức 5 x 3 - 7 x 2 + x chia hết cho 3 x n nên mỗi hạng tử của đa thức chia hết cho x n
=> hạng tử x – có số mũ nhỏ nhất của đa thức chia hết cho 3 x n
Do đó, x : x n ⇒ 0 ≤ x ≤ 1 . Vậy n ∈ {0; 1}
Đúng 0
Bình luận (0)
Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết:
a) x^ny^3:x^2y^n+1
b) x^2n+3:x^n-1
Các bạn giúp tớ với!!
Tìm n để mỗi phép chia sau là phép chia hết (n là số tự nhiên)
13
x
4
y
3
-
5
x
3
y
3
+
6
x
2
y...
Đọc tiếp
Tìm n để mỗi phép chia sau là phép chia hết (n là số tự nhiên) 13 x 4 y 3 - 5 x 3 y 3 + 6 x 2 y 2 : 5 x n y n
Vì đa thức 13 x 4 y 3 - 5 x 3 y 3 + 6 x 2 y 2 chia hết cho 5 x n y n nên mỗi hạng tử của đa thức trên chia hết cho 5 x n y n Do đó, hạng tử 6 x 2 y 2 chia hết cho 5 x n y n ⇒ 0 ≤ n ≤ 2 . Vậy n ∈ {0;1;2}
Đúng 0
Bình luận (0)
Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết: x 4 : x n
x 4 : x n = x 4 - n là phép chia hết nên 4 – n ≥ 0 ⇒ 0 ≤ n ≤ 4
suy ra: n ∈ {0; 1; 2; 3; 4}
Đúng 0
Bình luận (0)
Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết: 5 x n y 3 : 4 x 2 y 2
5 x n y 3 : 4 x 2 y 2 = 5/4 x n : x 2 y 3 : y 2 = 5/4 x n - 2 . y là phép chia hết
Suy ra: n – 2 ≥ 0 ⇒ n ≥ 2
Đúng 0
Bình luận (0)
Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết: x n y n + 1 : x 2 y 5
x n y n + 1 : x 2 y 5 = x n : x 2 y n + 1 : y 5 = x n - 2 . y n - 4 là phép chia hết
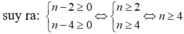
Đúng 0
Bình luận (0)
Bài 5.5: Tìm x: (2x-3)(x+1)+(4x^3-6x^2-6x):(-2x)18Bài 6.1: Tìm số tự nhiên n để: 5x^{n-2}:3x^2Bài 6.2: Tìm số tự nhiên n để đa thức x^{n-1}-3x^2:2x^2Bài 6.3: Tìm n ∈ N để phép tính chia sau là phép chia hết:3x^7y^7-4x^6y^6-5x^3y^3:(2x^ny^n)Trả lời nhanh giúp mìn nhóe!
Đọc tiếp
Bài 5.5: Tìm x: (2x-3)(x+1)+(4x\(^3\)-6x\(^2\)-6x):(-2x)=18
Bài 6.1: Tìm số tự nhiên n để: 5x\(^{n-2}\):3x\(^2\)
Bài 6.2: Tìm số tự nhiên n để đa thức x\(^{n-1}\)-3x\(^2\):2x\(^2\)
Bài 6.3: Tìm n ∈ N để phép tính chia sau là phép chia hết:
3x\(^7\)y\(^7\)-4x\(^6\)y\(^6\)-5x\(^3\)y\(^3\):(2x\(^n\)y\(^n\))
Trả lời nhanh giúp mìn nhóe!![]()
Bài 5.5:
\(\left(2x-3\right)\left(x+1\right)+\left(4x^3-6x^2-6x\right):\left(-2x\right)=18\)
\(\Leftrightarrow\left(2x^2+2x-3x-3\right)+2x\cdot\left(2x^2-3x-3\right):\left(-2x\right)=18\)
\(\Leftrightarrow2x^2-x-3-2x^2+3x+3=18\)
\(\Leftrightarrow2x=18\)
\(\Leftrightarrow x=\dfrac{18}{2}\)
\(\Leftrightarrow x=9\)
Đúng 1
Bình luận (0)
tìm số tự nhiên để mỗi phép chia sau là phép chia hết:
xnyn+1= x2y5
CHÚ Ý: TRÌNH BÀY ĐẦY ĐỦ
\(x^ny^{n+1}:x^2y^5=x^{n-2}.y^{n-4}\)
Để \(x^ny^{n+1}⋮x^2y^5\) thì \(\hept{\begin{cases}n-2\ge0\\n-4\ge0\end{cases}\Leftrightarrow}\hept{\begin{cases}n\ge2\\n\ge4\end{cases}}\Leftrightarrow n\ge4.\)
Tìm số tự nhiên n để phép chia sau là phép chia hết
\(\left(8x^2y^3-6x^4y^2+\frac{1}{2}x^3y^3\right):2x^{n-1}y^n\)










