Ta có

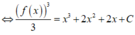
Ta có:  f ( 0 ) = 1 ⇒ 1 = 3 C

Xét hàm  trên [-2;1]

Ta có

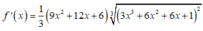
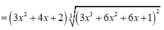
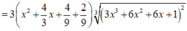
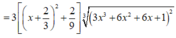
Nhận thấy f ' ( x ) > 0 ∀ x ∈ ℝ ⇒  Hàm số đồng biến trên (-2;1)

Suy ra  m a x - 2 ; 1   f ( x ) = f ( 1 ) = 16 3

Chọn đáp án C.

Đáp án: A.

Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2

⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.

Cách khác: Vì a = -1 nên parabol y = -x2 + 4x - 5 đạt cực đại tại đỉnh (2; -1). Vì vậy GTLN của hàm số trên đoạn [0;3] là y(2) = -1

Đáp án C

Chọn B

Câu 1:

$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$

Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$

Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.

Câu 2:

Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$

Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$

Với $x\in (1;3)$ thì hàm luôn nghịch biến

$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$

$\Rightarrow$ hàm không có min, max. 

Câu 3:

$y=x^2-4x-5$ có $a=1>0, b=-4; c=-5$ có trục đối xứng $x=\frac{-b}{2a}=2$

Do $a>0$ nên hàm nghịch biến trên $(-\infty;2)$ và đồng biến trên $(2;+\infty)$

Với $x\in (-1;4)$ vẽ BTT ta thu được $y_{\min}=f(2)=-9$

Đáp án B

Đáp án C

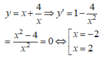
Ta có bảng biến thiên của hàm số y =  x + 4 x

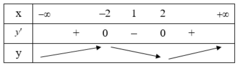
Nhìn vào bảng biến thiên ta thấy trên đoạn [1;2]