Cho hình chóp S.ABC. Lấy M, N, P lần lượt thuộc các cạnh SA, SB, SC thỏa mãn S A = 2 S M , S B = 3 S N , S C = 2 S P Biết thể tích S.ABC là a 3 2 Thể tích hình chóp S.MNP là
A. a 3 4
B. 2 a 3 7
C. a 3 24
D. a 3 16
Cho hình chóp S.ABC. Lấy M, N, P lần lượt thuộc các cạnh SA, SB, SC thỏa mãn Biết thể tích S.ABC là a 3 2 Thể tích hình chóp S.MNP là
A. a 3 4
B. 2 a 3 7
C. a 3 24
D. a 3 16
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và S A = a , S B = 2 a , S C = 3 a . Gọi M, N lần lượt là trung điểm của các cạnh SB, SC. Tính theo a thể tích hình chóp S.AMN.
A. a 3 4 .
B. 3 a 3 4 .
C. a 3 2 .
D. a 3
Phương pháp:
+) Thể tích của tứ diện vuông có độ dài các cạnh góc vuông là a, b, c là: V = 1 6 a b c
+) Sử dụng công thức tỉ số thể tích Simpson
Cách giải:
S.ABC là tứ diện vuông tại đỉnh S
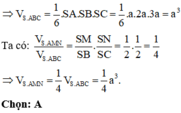
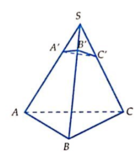
Cho khối chóp S.ABC có các điểm A', B', C' lần lượt thuộc các cạnh SA, SB, SC thỏa 3SA' = SA, 4SB' = SB, 5SC' = 3SC. Biết thể tích khối chóp S.A'B'C' bằng 5 ( c m 3 ). Tìm thể tích khối chóp S.ABC
A. 120 ( c m 3 )
B. 60 ( c m 3 )
C. 80 ( c m 3 )
D. 100 ( c m 3 )
Đáp án D
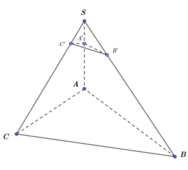
Key: Tính thể tích khối chóp B’.SA’C’ ta có:
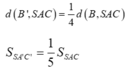
Suy ra:
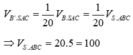
=> Chọn đáp án D.
Cho khối chóp S.ABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm A', B', C' sao cho ![]() . Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S'.A'B'C'. Khi đó tỷ số
. Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S'.A'B'C'. Khi đó tỷ số ![]() là:
là:
A. 12
B. 24
C. 1 12
D. 1 24
Cho hình chóp S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A', B', C' sao cho SA' = 2 3 SA, SB' = 5 6 SB, SC' = k k + 1 SC. Biết rằng V S . A ' B ' C ' = 1 2 V S . A B C . Lựa chọn phương án đúng.
A. k=6
B. k=7
C. k=8
D. k=9
Đáp án là D
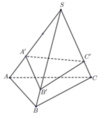
Ta có 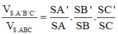
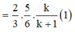
Theo giả thiết 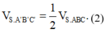
Từ (1) và (2) suy ra ![]()
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm
A', B', C' sao cho SA' = 1 3 SA , SB' = 1 3 SB, SC' = 1 3 SC. Gọi V và V'
lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C'. Khi đó tỉ số V ' V là
![]()
![]()
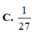
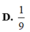
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, S A = S B = S C = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
A. a 3 3
B. a 3
C. a 3 24
D. a 3 12
Đáp án C
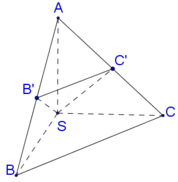
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.
Ta có:
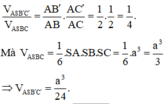
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SA=SB=SC=a. Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC với SA ⊥ SB , SB ⊥ SC , SC ⊥ SA ; SA = SB = SC = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB, AC. Thể tích của hình chóp S.AB′C′ là
A. a 3 24
B. a 3
C. a 3 3
D. a 3 12