Tìm tập hợp nghiệm của bất phương trình sau:
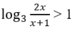
A. (- ∞ ; -3) B. (-1; + ∞ )
C. (- ∞ ; -3)∪(-1; + ∞ ) D. (-3; -1)
Những câu hỏi liên quan
Tìm \(D = E \cap G\) biết E và G lần lượt là tập nghiệm của hai bất phương trình trong mỗi trường hợp sau:
a) \(2x + 3 \ge 0\) và \( - x + 5 \ge 0\)
b) \(x + 2 > 0\) và \(2x - 9 < 0\)
a) Ta có: \(2x + 3 \ge 0 \Leftrightarrow x \ge \frac{{ - 3}}{2}\)
\( \Rightarrow \) Tập hợp E là: \(E = \left\{ {x \in \mathbb{R}|x \ge \frac{{ - 3}}{2}} \right\}\)
và \( - x + 5 \ge 0 \Leftrightarrow x \le 5\)
\( \Rightarrow \) Tập hợp G là \(G = \left\{ {x \in \mathbb{R}|x \le 5} \right\}\)
\( \Rightarrow E \cap G = \){\(x \in \mathbb{R}|\)\(x \ge \frac{{ - 3}}{2}\) và \(x \le 5\)} \( = \left\{ {x \in \mathbb{R}|\frac{{ - 3}}{2} \le x \le 5} \right\}\)
Vậy tập hợp D \( = \left\{ {x \in \mathbb{R}|\frac{{ - 3}}{2} \le x \le 5} \right\} = [\frac{{ - 3}}{2}; 5]\)
b) Ta có: \(x + 2 > 0 \Leftrightarrow x>-2\)
\( \Rightarrow E = \left\{ {x \in \mathbb{R}|x >-2 }\right\}\)
và \( 2x - 9 < 0 \Leftrightarrow x < \frac{9}{2}\)
\( \Rightarrow G = \left\{ {x \in \mathbb{R}|x < \frac{9}{2}} \right\}\)
\( \Rightarrow E \cap G = \){\(x \in \mathbb{R}|\)\(x > -2 \) và \(x < \frac{9}{2}\)} \( = \left\{ {x \in \mathbb{R}|-2<x< {9\over 2} } \right\}\)
Vậy \( D= \left\{ {x \in \mathbb{R}|-2<x< {9\over 2}} \right\}=(-2;{9\over 2})\)
Đúng 0
Bình luận (0)
Tìm tập hợp nghiệm của bất phương trình sau:
Tìm tập hợp nghiệm S của bất phương trình
l
o
g
π
4
(
x
2
+
1
)
l
o
g
π
4
(
2
x
+
4
)
.
A.
S
-
2
;
...
Đọc tiếp
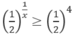
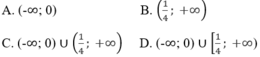
Tìm tập hợp nghiệm S của bất phương trình l o g π 4 ( x 2 + 1 ) < l o g π 4 ( 2 x + 4 ) .
A. S = - 2 ; - 1
B. S = - 2 ; + ∞
C. S = 2 ; + ∞ ∪ - 2 ; - 1
D. S = 3 ; + ∞
Tìm tập hợp tất cả các nghiệm thực của bất phương trình
9
7
3
x
−
2
x
2
≥
9
7
.
A.
x
∈
1
2
;
1
B. ...
Đọc tiếp
Tìm tập hợp tất cả các nghiệm thực của bất phương trình 9 7 3 x − 2 x 2 ≥ 9 7 .
A. x ∈ 1 2 ; 1
B. x ∈ 1 2 ; 1
C. x ∈ − ∞ ; 1 2 ∪ 1 ; + ∞
D. x ∈ − ∞ ; 1 2 ∪ 1 ; + ∞
Đáp án A
9
7
3
x
−
2
x
2
≥
9
7
⇔
3
x
−
2
x
2
≥
1
⇔
2
x
2
−
3
x
+
1
≤
0
⇔
1
2
≤
x
≤
1
Đúng 0
Bình luận (0)
Tìm tập hợp nghiệm của bất phương trình:
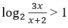
A. (- ∞ ; -2) B. (4; ∞ )
C. (- ∞ ; -2) ∪ (4; + ∞ ) D. (-2;4)
Gọi S là tập hợp các nghiệm nguyên của bất phương trình 1 3 x 2 - 3 x - 10 . Tìm số phần tử của S.
A. 11
B. 10
C. 9
D. 1
Tìm tập hợp nghiệm của bất phương trình:
log
2
3
x
x
+
2
1
A. (-
∞
; -2) B. (4; +
∞
)C. (-
∞
; -2)
∪
(4; +
∞
) D...
Đọc tiếp
Tìm tập hợp nghiệm của bất phương trình: log 2 3 x x + 2 > 1
A. (- ∞ ; -2) B. (4; + ∞ )
C. (- ∞ ; -2) ∪ (4; + ∞ ) D. (-2;4)
Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:
a) Tập hợp \(A = \{1;2;3;6;9;18\} \)
b) Tập hợp \(B\) các nghiệm của bất phương trình \(2x+1>0\)
c) Tập hợp \(C\) các nghiệm của phương trình \(2x-y=6\)
a) A là tập hợp các ước nguyên dương của 18.
\(A = \{x \in \mathbb N | x \in U(18)\} \)
b) \(B = \{x \in \mathbb R | 2x+1>0\} \)
c) C là tập hợp các cặp số (x;y) thỏa mãn \(2x-y=6\).
\(C = \{(x;y)| 2x-y=6\} \)
Đúng 0
Bình luận (0)
Tìm tập hợp nghiệm của bất phương trình sau:
log
3
2
x
x
+
1
A. (-
∞
; -3) B. (-1; +
∞
)C. (-
∞
; -3)
∪
(-1; +
∞
) D. (-3; -1)
Đọc tiếp
Tìm tập hợp nghiệm của bất phương trình sau:
log 3 2 x x + 1
A. (- ∞ ; -3) B. (-1; + ∞ )
C. (- ∞ ; -3) ∪ (-1; + ∞ ) D. (-3; -1)