Hãy so sánh x với 1, biết rằng: log 1 3 x = 1,7
Những câu hỏi liên quan
Hãy so sánh x với 1, biết rằng:
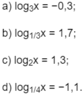
Hãy so sánh x với 1, biết rằng: log 2 x = 1,3
Hãy so sánh x với 1, biết rằng: log 1 4 x = -1,1
Hãy so sánh x với 1, biết rằng: log 3 x = −0,3
SGK Cánh Diều
13 tháng 8 2023 lúc 21:07
Hoạt động 5
Cho ba số thực dương a, b, c với \(a \ne 1\,;\,c \ne 1\)
a) Bằng cách sử dụng tính chất \(b = {a^{{{\log }_a}b}}\), chứng tỏ rằng \({\log _c}b = {\log _a}b.{\log _c}a\)
b) So sánh \({\log _a}b\,\,\,và \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
a) \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {a^{{{\log }_c}b}} = {a^{{{\log }_a}b.{{\log }_c}a}} \Leftrightarrow {c^{{{\log }_c}b}} = {\left( {{c^{{{\log }_c}a}}} \right)^{{{\log }_a}b}} \Leftrightarrow b = {a^{{{\log }_a}b}} \Leftrightarrow b = b\) (luôn đúng)
Vậy \({\log _c}b = {\log _a}b.{\log _c}a\)
b) Từ \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
Đúng 0
Bình luận (0)
so sánh các cặp số
a) |-3| và |3|
b) |1,3| và |-0,5|
c)|-100| và |20|
2 tìm x, biết :
a) |x-1,7|= 2,3
b) |x + 3/4|- 1/3 =0
Bài 1 rất dễ nên bạn tự làm nhé
Bài 2:
a) \(\left|x-1,7\right|=2,3\)
\(\Rightarrow x-1,7=\pm2,3\)
+) \(x-1,7=2,3\Rightarrow x=4\)
+) \(x-1,7=-2,3\Rightarrow x=-0,6\)
Vậy x = 4 hoặc x = -0,6
b) \(\left|x+\frac{3}{4}\right|-\frac{1}{3}=0\)
\(\Rightarrow\left|x+\frac{3}{4}\right|=\frac{1}{3}\)
\(\Rightarrow x+\frac{3}{4}=\pm\frac{1}{3}\)
+) \(x+\frac{3}{4}=\frac{1}{3}\Rightarrow x=\frac{-5}{12}\)
+) \(x+\frac{3}{4}=-\frac{1}{3}\Rightarrow x=\frac{-13}{12}\)
Vậy \(x=\frac{-5}{12}\) hoặc \(x=\frac{-13}{12}\)
Đúng 0
Bình luận (0)
a, = nhau
b, 1.3> hơn
c, 100> hơn
2
a,ta suy ra được x-1.7=2.3 hoặc x-1.7=-2.3
từ đó bạn tự tính nhé
b, ta suy ra được x+3/4=1/3 hoặc x+3/4=-1/3
từ đó bạn tự tính nhé
Đúng 0
Bình luận (0)
Bài 1:cho hàm số f(x) xác định với mọi x thuộc R .Biết rằng với mọi x khác 0 ta đều có
\(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\) .Tính f(2)
Bài 2:Tính tổng T=\(\frac{2}{2^1}+\frac{3}{2^2}+\frac{4}{2^3}+...+\frac{2015}{2^{2014}}\).Hãy so sánh T với 3
Cho x=a/b; y= c/d; z= m/n
Trong đó m= (a+c)/2; n= (b+d)/2
a) Biết x khác y hãy so sánh x với z và y với z
b) Hãy so sánh y với t biết t= a+m/b+m và ad - bc= 1; cn - dm = 1
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 19:21
Trong các hàm số sau, những hàm số nào là hàm số lôgarit? Khi đó hãy chỉ ra cơ số.
a) \(y = {\log _{\sqrt 3 }}x;\)
b) \(y = {\log _{{2^{ - 2}}}}x;\)
c) \(y = {\log _x}2;\)
d) \(y = {\log _{\frac{1}{x}}}5.\)
Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)
Đúng 1
Bình luận (0)