Tính thể tích V của khối hộp chữ nhật ABCD.A'B'C'D' biết AB=a, AD=2a, AC'=a 14 .
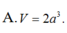
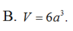
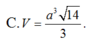
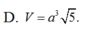
Tính thể tích V của khối hộp chữ nhật A B C D . A ' B ' C ' D ' biết A B = a , A D = 2 a , A C ' = a 14 .
A. V = 2 a 3
B. V = 6 a 3
C. V = a 3 14 3
D. V = a 3 5
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = 2 a , A C ' = 2 3 a . Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’.
A. V = 2 6 a 3
B. V = 2 6 3 a 3
C. V = 3 2 a 3
D. V = 6 a 3
Đáp án C
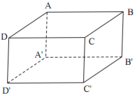
Phương pháp:
Thể tích khối hộp chữ nhật: V = abc
Cách giải:
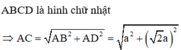
= 3 a
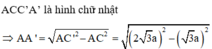
= 3a
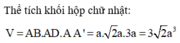
Cho hình hộp chữ nhật ABCD.A'B'C'D' có A D = 2 a , A C ' = 2 3 a . Tính theo a thể tích V của khối hộp ABCD.A'B'C'D'
A. V = 2 6 a 3
B. V = 2 6 a 3 3
C. V = 3 2 a 3
D. V = 6 a 3
Đáp án C
Ta có: A A ' = 2 3 a 2 − a 2 − 2 a 2 = 3 a
Thể tích khối hộp là: V = A A ' . S A B C D = 3 a . a 2 a = 3 2 a 3
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = 2a, AC' = 6 a. Thể tích khối hộp chữ nhật ABCD.A'B'C'D' bằng:
A. 3 a 3 3
B. 2 a 3 3
C. 2 a 3
D. 2 3 a 3
Phương pháp:
Công thức tính thể tích khối hộp chữ nhật ABCD.A'B'C'D' là V = AA'.AB.AD
Cách giải:
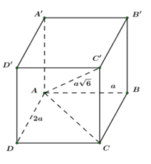
Ta có: ![]() (định lý Pitago)
(định lý Pitago)
Xét tam giác ACC’ vuông tại C ta có:
![]()
![]()
![]()
Chọn C.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD= 2 a . Tính theo a thể tích V của khối hộp ABCD.A'B'C'D'
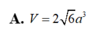
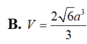
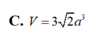
Tính thể tích V của khối hộp chữ nhật ABCD.A'B'C'D', biết AB = a, AD = a 2 và AC' hợp với đáy một góc 60°.
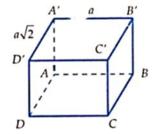
A. V = 2 a 3 6
B. V = a 3 2
C. V = 3 a 3 2
D. V = 3 a 3 2 2
Câu 21: Cho khối hộp chữ nhật ABCD.A'B'C'D'. Biết AC=5, AB'=7, AD'=8. Tính thể tích khối hộp chữ nhật này?
Câu 36: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a, \(AD=a\sqrt{3}\). SA\(\perp\)(ABCD), SA=2a. Gọi (P) là mặt phẳng qua A và vuông góc với cạnh bên SC, cắt các cạnh bên SB,SC,SD lần lượt tại E,F,H. Tính thể tích khối chóp S.AEFH?
Hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = 2a, AA' = a 2 . Tính thể tích V của A'BB'D.
A. V = a 3 3 2
B. V = 2 a 3 2 3
C. V = a 3 2
D. V = a 3 2 3
Cho khối hộp chữ nhật A B C D . A ' B ' C ' D ' có A C = B ' D ' = a , A B ' = C D ' = b , A D ' = B ' C = c . Thể tích của khối hộp chữ nhật A B C D . A ' B ' C ' D ' là
A. 1 8 − a 2 + b 2 + c 2 a 2 − b 2 + c 2 a 2 + b 2 − c 2
B. 1 2 2 b 2 + c 2 a 2 + c 2 a 2 + b 2
C. 3 a b c
D. 1 2 2 − a 2 + b 2 + c 2 a 2 − b 2 + c 2 a 2 + b 2 − c 2
Đáp án D
Gọi độ dài các cạnh A A ' , A D , A B lần lượt là x , y , z . Ta có
y 2 + z 2 = a 2 1 z 2 + x 2 = b 2 2 x 2 + y 2 = c 2 3 ⇒ x 2 + y 2 + z 2 = 1 2 a 2 + b 2 + c 2 4
Trừ vế theo vế (4) cho (1), (2), (3) ta có
x 2 = 1 2 − a 2 + b 2 + c 2 ; y 2 = 1 2 a 2 − b 2 + c 2 ; z 2 = 1 2 a 2 + b 2 − c 2
Thể tích khối hộp chữ nhật là
1 2 2 − a 2 + b 2 + c 2 a 2 − b 2 + c 2 a 2 + b 2 − c 2