Trong các loại hình sau: Tứ diện đều; hình chóp tứ giác đều; hình lăng trụ tam giác đều; hình hộp chữ nhật, loại hình nào có ít mặt phẳng đối xứng nhất
A. Tứ diện đều
B. Hình chóp tứ giác đều
C. Hình lăng trụ tam giác đều
D. Hình hộp chữ nhật
Trong các loại hình sau: Tứ diện đều; hình chóp tứ giác đều; hình lăng trụ tam giác đều; hình hộp chữ nhật, loại hình nào có ít mặt phẳng đối xứng nhất.
A. Tứ diện đều
B. Hình chóp tứ giác đều
C. Hình lăng trụ tam giác đều
D. Hình hộp chữ nhật
Đáp án D
Tứ diện đều có 6 mặt phẳng đối xứng
Hình chóp tứ giác đều có 4 mặt phẳng đối xứng
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng
Hình hộp chữ nhật có 3 mặt phẳng đối xứng
Trong các loại hình sau: Tứ diện đều, hình chóp tứ giác đều, hình lăng trụ tam giác đều, hình hộp chữ nhật, loại hình nào có ít mặt phẳng đối xứng nhất?
A. Tứ diện đều
B. Hình chóp tứ giác đều
C. Hình lăng trụ tam giác đều
D. Hình hộp chữ nhật.
Đáp án D
Tứ diện đều có 6 mặt phẳng đối xứng là các mặt phẳng đi qua một cạnh và trung điểm của cạnh đối.
Hình chóp tứ giác đều có 4 mặt phẳng đối xứng, trong đó 2 mặt phẳng đối xứng là những mặt phẳng đi qua đỉnh và đường chéo của mặt đáy, 2 mặt phẳng đối xứng là những mặt phẳng đi qua đỉnh và đường thẳng nối trung điểm của hai cạnh đáy.
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng, trong đó 3 mặt phẳng đối xứng là những mặt phẳng đi qua hai trung điểm của hai cạnh đáy song song và cạnh bên không đồng phẳng với hai cạnh đáy đó, 1 mặt đối xứng đi qua trung điểm của 3 cạnh bên.
Hình hộp chữ nhật có 3 mặt đối xứng là các mặt phẳng đi qua các trung điểm của 4 cạnh song song.
Cắt miếng bìa hình tam giác đều cạnh bằng 1 như hình bên và gấp theo các đường kẻ, sau đó dán các mép lại để được hình tứ diện đều. Tính thể tích V của hình tứ diện tạo thành.

A. V = 2 96
B. V = 3 16
C. V = 3 32
D. V = 2 12
Trong tất cả các loại hình đa diện đều sau đây, hình nào có số mặt nhiều nhất?
A. Loại {3;4}
B. Loại {5;3}
C. Loại {4;3}
D. Loại {3;5}.
Đáp án D
Hình đa diện đều loại {3;5} có 20 mặt, là hình đa diện đều có số mặt nhiều nhất.
Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đều OA = 8cm,BC = CD = 6cm
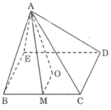
Vì AO là đường cao hình chóp nên ΔAOM vuông tại O.
Ta có OM = 1/2 CD = 3 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
A M 2 = A O 2 + O M 2 = 8 2 + 3 2 = 73
Suy ra: AM = 73 (cm)
Ta có: S x q = Pd = 6.2. 73 = 12 73 ( c m 2 )
S đ á y = 6.6 = 36 ( c m 2 )
Vậy S T P = S x q + S đ á y = 12√73 +36 ≈ 138,5( c m 2 )
Chứng minh rằng tâm của các mặt của các hình tứ diện đều là các đỉnh của một hình tứ diện đều ?
Cho hình tứ diện đều ABCD, cạnh bằng a. Gọi E, F, I, J lần lượt là tâm của các mặt ABC, ABD, ACD, BCD (H.11).
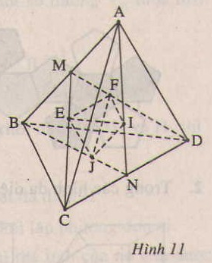
Vì ![]() , nên \(\dfrac{EF}{CD}=\dfrac{1}{3}\)
, nên \(\dfrac{EF}{CD}=\dfrac{1}{3}\)
Suy ra ![]() .
.
Tương tự, các cạnh khác của tứ diện EFIJ đều bằng ![]() .
.
Do đó tứ diện EFIJ là một tứ diện đều.
Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đều cạnh đáỵ 1m, chiều cao hình chóp 50cm
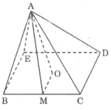
Hình chóp tứ giác đều, cạnh đáy bằng 1m, chiếu cao hình chóp bằng 0,5m.
Tương tự hình vẽ câu a ta có AM Δ BC.
Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.
Áp dụng định li Pi-ta-go vào tam giác vuông AOM,ta có:
A M 2 = O A 2 + O M 2 = 0 , 5 2 + 0 , 5 2 = 0 , 5
Suy ra: AM = 0,5 cm
Ta có: S x q =1.2. 0 , 5 =2 0 , 5 ( m 2 )
S đ á y = 1.1=1( m 2 )
Vậy S T P = S x q + S đ á y = 2 0 , 5 + 1 ≈ 2,4( m 2 )
Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đều cạnh đáỵ 20cm, chiều cao hình chóp 7cm
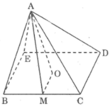
Hình chóp tứ giác đều, cạnh đáy bằng 20cm, chiều cao hình chóp bằng 7cm
Tương tự hình vẽ câu a ta có MA Δ BC
Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
A M 2 = O A 2 + O M 2 = 49 + 100 = 149
Suy ra: AM = 149 cm
Ta có: S x q =20.2. 149 =40 149 ( c m 2 )
S đ á y = 20.20= 400( c m 2 )
Vậy S T P = S x q + S đ á y = 40 149 +400 ≈ 888,3( c m 2 )
Cho các khối đa diện đều như hình vẽ sau đây. Khối đa diện đều loại {3;5} là hình nào?
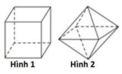
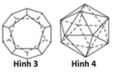
A. Hình 4
B. Hình 1
C. Hình 2
D. Hình 3