Các câu hỏi tương tự
Cho hình đa diện như hình vẽ, trong đó các cạnh AA’, BB’, CC’ đều vuông góc với (ABC), tam giác ABC đều cạnh a và
A
A
B
B
1
2
C
C
a
. Tính theo a thể tích V của khối đa diện đó. A.
V
a
3
3
6
....
Đọc tiếp
Cho hình đa diện như hình vẽ, trong đó các cạnh AA’, BB’, CC’ đều vuông góc với (ABC), tam giác ABC đều cạnh a và A A ' = B B ' = 1 2 C C ' = a . Tính theo a thể tích V của khối đa diện đó.
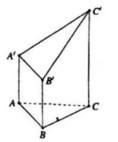
A. V = a 3 3 6 .
B. V = a 3 3 3 .
C. V = 4 a 3 3 3 .
D. V = 3 a 3 3 4 .
Trong một cuộc thi làm đồ dùng học tập do trường phát động, bạn An nhờ bố làm một hình chóp tứ giác đều bằng cách lấy một mảnh tôn hình vuông ABCD có cạnh bằng 5cm, cắt mảnh tôn theo các tam cân AEB, CGD, DHA; sau đó gò các tam giác AEH, BEF, CFG, DGH sao cho bốn đỉnh A, B, C, D trùng nhau tạo thành khối chóp tứ giác đều. Thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng: A.
4
10
3
.
B. ...
Đọc tiếp
Trong một cuộc thi làm đồ dùng học tập do trường phát động, bạn An nhờ bố làm một hình chóp tứ giác đều bằng cách lấy một mảnh tôn hình vuông ABCD có cạnh bằng 5cm, cắt mảnh tôn theo các tam cân AEB, CGD, DHA; sau đó gò các tam giác AEH, BEF, CFG, DGH sao cho bốn đỉnh A, B, C, D trùng nhau tạo thành khối chóp tứ giác đều. Thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng:
A. 4 10 3 .
B. 4 10 5 .
C. 8 10 3 .
D. 8 10 5 .
Người ta cắt một tờ giấy hình vuông có cạnh bằng
2
để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối chóp để thể tích của nó lớn nhất. A.
2
5
B.
2
5
C. 1 D.
4
5
Đọc tiếp
Người ta cắt một tờ giấy hình vuông có cạnh bằng 2 để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối chóp để thể tích của nó lớn nhất.
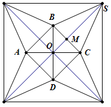
A. 2 5
B. 2 5
C. 1
D. 4 5
Từ một miếng tôn hình tam giác đều cạnh
3
, người ta dùng để chế tạo một thùng hình trụ không đáy có thể tích V bằng cách cắt ra một hình chữ nhật như hình vẽ. Giá trị lớn nhất của V bằng bao nhiêu lít? (kết quả làm tròn đến hàng phần trăm) A. 45,92 B. 40,72. C. 65,03 D. 53,05
Đọc tiếp
Từ một miếng tôn hình tam giác đều cạnh 3 , người ta dùng để chế tạo một thùng hình trụ không đáy có thể tích V bằng cách cắt ra một hình chữ nhật như hình vẽ. Giá trị lớn nhất của V bằng bao nhiêu lít? (kết quả làm tròn đến hàng phần trăm)
A. 45,92
B. 40,72.
C. 65,03
D. 53,05
Cắt ba góc của một tam giác đều cạnh a các đoạn bằng
x
,
0
x
a
2
phần còn lại là một tam giác đều bên ngoài là các hình chữ nhật, rồi gấp các hình chữ nhật lại tạo thành khối lăng trụ tam giác đều như hình vẽ. Tìm độ dài x để thể tích khối lăng trụ lớn nhất. A.
x
a
3...
Đọc tiếp
Cắt ba góc của một tam giác đều cạnh a các đoạn bằng x , 0 < x < a 2 phần còn lại là một tam giác đều bên ngoài là các hình chữ nhật, rồi gấp các hình chữ nhật lại tạo thành khối lăng trụ tam giác đều như hình vẽ. Tìm độ dài x để thể tích khối lăng trụ lớn nhất.
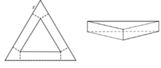
A. x = a 3
B. x = a 4
C. x = a 5
D. x = a 6
Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng 2a. Tính thể tích V của khối nón S có đỉnh và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD. A.
V
π
3
a
3
6
B.
V
π
2
a
3...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng 2a. Tính thể tích V của khối nón S có đỉnh và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD.
A. V = π 3 a 3 6
B. V = π 2 a 3 3
C. V = π 2 a 3 6
D. V = π 3 a 3 3
Cho hình chóp tứ giác đều S.ABCD có thể tích V, có O là tâm của đáy. Lấy M là trung điểm của cạnh bên SC. Thể tích khối tứ diện ABMO bằng
A. V 4
B. V 2
C. V 16
D. V 8
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB a,
E
F
B
^
30
°
và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF A.
V
4
/
3
a
3
B. V 10/9
a
3
C....
Đọc tiếp
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB= a, E F B ^ = 30 ° và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF
A. V = 4 / 3 a 3
B. V= 10/9 a 3
C. V= 4/3 π a 3
D. V= 10/9 π a 3
Cho hình chóp S.ABCD có cạnh bên
S
A
a
0
a
3
và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD. A.
V
a
3
-
a
2
3
B. đ...
Đọc tiếp
Cho hình chóp S.ABCD có cạnh bên S A = a 0 < a < 3 và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD.
A. V = a 3 - a 2 3
B. đáp án khác
C. 2 2
D. 2